Euclid continuity

Let's talk about one of the simplest, if not trivial, subjects in the oldest and best-established branch of mathematics: rectangle area in elementary Euclid geometry. The story contains two twists and an anecdote.

We all know that the area of a rectangle or a parallelogram is a product of its base and height, and the area of a triangle is half of that (areas of a parallelogram, a triangle and a rectangle can all be reduced to each other by a device invented by Euclid), but Euclid would not say that: the idea that measures such as lengths, areas or volumes can be multiplied is alien to him, as it still is to Galileo. There is a huge body of literature on the evolution that culminated with our modern notion of number, unifying disparate incompatible numbers and measures of the past mathematics, enough to say that before Newton-Leibniz time, ratios and fractions were not the same.

Euclid instead says (Book VI, prop. I, hereinafter quotes from the Elements are given as <Greek | English | Russian>):

<τὰ τρίγωνα καὶ τὰ παραλληλόγραμμα, τὰ ὑπὸ τὸ αὐτὸ ὕψος ὄντα πρὸς ἄλληλά ἐστιν ὡς αἱ βάσεις. | Triangles and parallelograms, which are under the same height are to one another as their bases.| Треугольники и параллелограммы под одной и той же высотой, [относятся] друг к другу как основания.>

Given rectangles \(ABCD\) and \(AEFD\) with the same height \(AD\), we want to prove that the ratio of their areas is the same as of their bases: \(\Delta(ABCD)/\Delta(AEFD) = AB/AE\).

First, consider a case where the bases are commensurable, that is, as we would say \(AB/AE = n/m\) for some inetegers \(n\) and \(m\), or as Euclid would say, there is a length \(AX\), such that \(AB = n \cdot AX\) (that is, the interval \(AB\) is equal to \(n\) times extended interval \(AX\)) and \(AE = m \cdot AX\). Then, \(ABCD\) can be divided into \(n\) equal rectangles \(AXYD\) with the height \(AD\) the base \(AX\) and the area \(\Delta_0\), and \(AEFD\) can be divided into \(m\) of them. 

Then, $$\begin{array}{lclclcl} \Delta(ABCD) & = & \Delta(AXYD) & + & \Delta(XX'Y'Y) & + & \ldots\\ & = & n \cdot \Delta_0, & & & & \end{array}$$ and $$\begin{array}{lclclcl} \Delta(AEFD) & = & \Delta(AXYD) & + & \Delta(XX'Y'Y) & + & \ldots \\ & = & m \cdot \Delta_0 \end{array}$$ so that \(\Delta(ABCD)/\Delta(AEFD) = n/m = AB/AE\), as required.

Starting from the early twentieth century, the rigorous proof of the remaining incommensurable case in a school-level exposition typically involves some form of a limit and is based on an implicit or explicit continuity axiom, usually equivalent to Cavaliery principle.

There is, however, a completely elementary, short and elegant proof, that requires no additional assumptions. This proof is used by Legendre (I don't know who is the original author) in his Elements, Éléments de géométrie. Depending on the edition, it is Proposition III in either Book III (p. 100) or Book IV (page 90, some nineteenth-century editions, especially with "additions and modifications by M. A. Blanchet", are butchered beyond recognition, be careful). The proof goes like this:

For incommensurable \(AB\) and \(AE\) consider the ratio \(\Delta(ABCD)/\Delta(AEFD)\). If \(\Delta(ABCD)/\Delta(AEFD) = AB/AE\) we are done. If \(\Delta(ABCD)/\Delta(AEFD)\) is not equal to \(AB/AE\), it is instead equal to \(AB/AO\) and either \(AE < AO\) or \(AE > AO\). Consider the first case (the other one is similar).

The points at the base are in order \(A\), then \(B\), then \(E\), then \(O\).

Divide \(AB\) into \(n\) equal intervals, each shorter that \(EO\). This requires what we now call the Archimedes-Eudoxus axiom and which is implied by Definition IV of Book V:

<λόγον ἔχειν πρὸς ἄλληλα μεγέθη λέγεται, ἃ δύναται πολλαπλασιαζόμενα ἀλλήλων ὑπερέχειν. | Magnitudes are said to have a ratio to one another which can, when multiplied, exceed one another. | Величины имеют отношение между собой, если они взятые кратно могут превзойти друг друга.>

Then continue dividing \(BE\), until we get to a point \(I\) outside of \(BE\), but within \(EO\) (because the interval is shorter than \(EO\)). The points are now in order \(A\), then \(B\), then \(E\), then \(I\), then \(O\).

\(AB\) and \(AI\) are commensurable, so \(\Delta(ABCD)/\Delta(AIKD) = AB/AI\). Also, \(\Delta(ABCD)/\Delta(AEFD) = AB/AO\), so \(\Delta(AIKD)/\Delta(AEFD) = AI/AO\). By construction \(AI < AO\), hence \(\Delta(AIKD) < \Delta(AEFD)\), but \(AEFD\) is a proper part of \(AIKD\), so \(\Delta(AEFD) < \Delta(AIKD)\). Contradiction.

Step back and look at the structure of these two proofs from the modern perspective. Fix the height and let \(\Delta(X)\) be the area of the rectangle with the base of length \(X\). By an assumption that we would call "additivity of measure" \(\Delta(X+Y) = \Delta(X) + \Delta(Y)\), that is, \(\Delta\) is an additive function. A general and easy-to-establish fact (mentioned with remarkable persistency on this blog [Unexpected isomorphism], [The Hunt for Addi(c)tive Monster]) is that any additive function is linear on rationals, that is, \(\Delta(n/m \cdot X) = n/m \cdot \Delta(X)\). This corresponds to the "commensurable" part of the proofs. To complete a proof we need linearity: \(\Delta(X) = X \cdot H\), where \(H = \Delta(1)\). But additive functions are not necessarily linear. To obtain linearity, an additional condition is needed. The traditional proof uses continuity: a continuous (at least at one point) additive function is necessarily linear.

Legendre's proof uses monotonicity: a monotonic additive function is always linear. This is clever, because monotonicity is not an additional assumption: it follows from the already assumed positivity of measure: If \(Y > X\), then \(\Delta(Y) = \Delta(X + (Y - X)) = \Delta(X) + \Delta(Y - X) > \Delta(X)\), as \(\Delta(Y - X) > 0\).

How does the original Euclid's proof look like? (He proves the triangle version, which is similar to rectangles.)

Wait... It is unbelievably short, especially given that the Elements use no notation and spell everything in words and it covers both triangles and parallelograms. It definitely has no separate "commensurable" and "imcommensurable" parts. How is this possible?

The trick is in the definition of equal ratios, Def. V of Book V:

<ἐν τῷ αὐτῷ λόγῳ μεγέθη λέγεται εἶναι πρῶτον πρὸς δεύτερον καὶ τρίτον πρὸς τέταρτον, ὅταν τὰ τοῦ πρώτου καὶ τρίτου ἰσάκις πολλαπλάσια τῶν τοῦ δευτέρου καὶ τετάρτου ἰσάκις πολλαπλασίων καθ᾽ ὁποιονοῦν πολλαπλασιασμὸν ἑκάτερον ἑκατέρου ἢ ἅμα ὑπερέχῃ ἢ ἅμα ἴσα ᾖ ἢ ἅμα ἐλλείπῃ ληφθέντα κατάλληλα. | Magnitudes are said to be in the same ratio, the first to the second and the third to the fourth, when, if any equimultiples whatever are taken of the first and third, and any equimultiples whatever of the second and fourth, the former equimultiples alike exceed, are alike equal to, or alike fall short of, the latter equimultiples respectively taken in corresponding order. | Говорят, что величины находятся в том же отношении: первая ко второй и третья к четвёртой, если равнократные первой и третьей одновременно больше, или одновременно равны, или одновременно меньше равнократных второй и четвёртой каждая каждой при какой бы то ни было кратности, если взять их в соответственном порядке.>

In modern notation this means that

$$\Delta_1 / \Delta_2 = b_1 / b_2 \equiv (\forall n\in\mathbb{N}) (\forall m\in\mathbb{N}) (n\cdot\Delta_1 \gtreqqless m\cdot\Delta_2 = n\cdot b_1 \gtreqqless m\cdot b_2),$$

where \(\gtreqqless\) is "FORTRAN 3-way comparison operator" (aka C++ spaceship operator):

$$ X \gtreqqless Y = \begin{cases} -1, & X < Y\\ 0, & X = Y\\ +1, & X > Y \end{cases} $$

This looks like a rather artificial definition of ratio equality, but with it the proof of Proposition I and many other proofs in Books V and VI, become straightforward or even forced.

The approach of selecting the definitions to streamline the proofs is characteristic of abstract twentieth-century mathematics and it is amazing to see it in full force in the earliest mathematical text we have.

I'll conclude with the promised anecdote (unfortunately, I do not remember the source). An acquaintance of Newton having met him in the Cambridge library and found, on inquiry, that Newton is reading the Elements, remarked something to the effect of "But Sir Isaac, haven't your methods superseded and obsoleted Euclid?". This is one of the two recorded cases when Newton laughed.

When people used to care about the quality of presentation

 

From Errata to Dijsktra's A Primer of Algol 60 Programming.

usched: update

Update for the previous post about stackswap coroutine implementation usched.

To recap, usched is an experimental (and very simple, 120LOC) coroutine implementation different from stackful and stackless models: coroutines are executed on the native stack of the caller and when the coroutine is about to block its stack is copied into a separately allocated (e.g., in the heap) buffer. The buffer is copied back onto the native stack when the coroutine is ready to resume.

I added a new scheduler ll.c that distributes coroutines across multiple native threads and then does lockless scheduling within each thread. In the benchmark (the same as in the previous post), each coroutine in the communicating cycle belongs to the same thread.

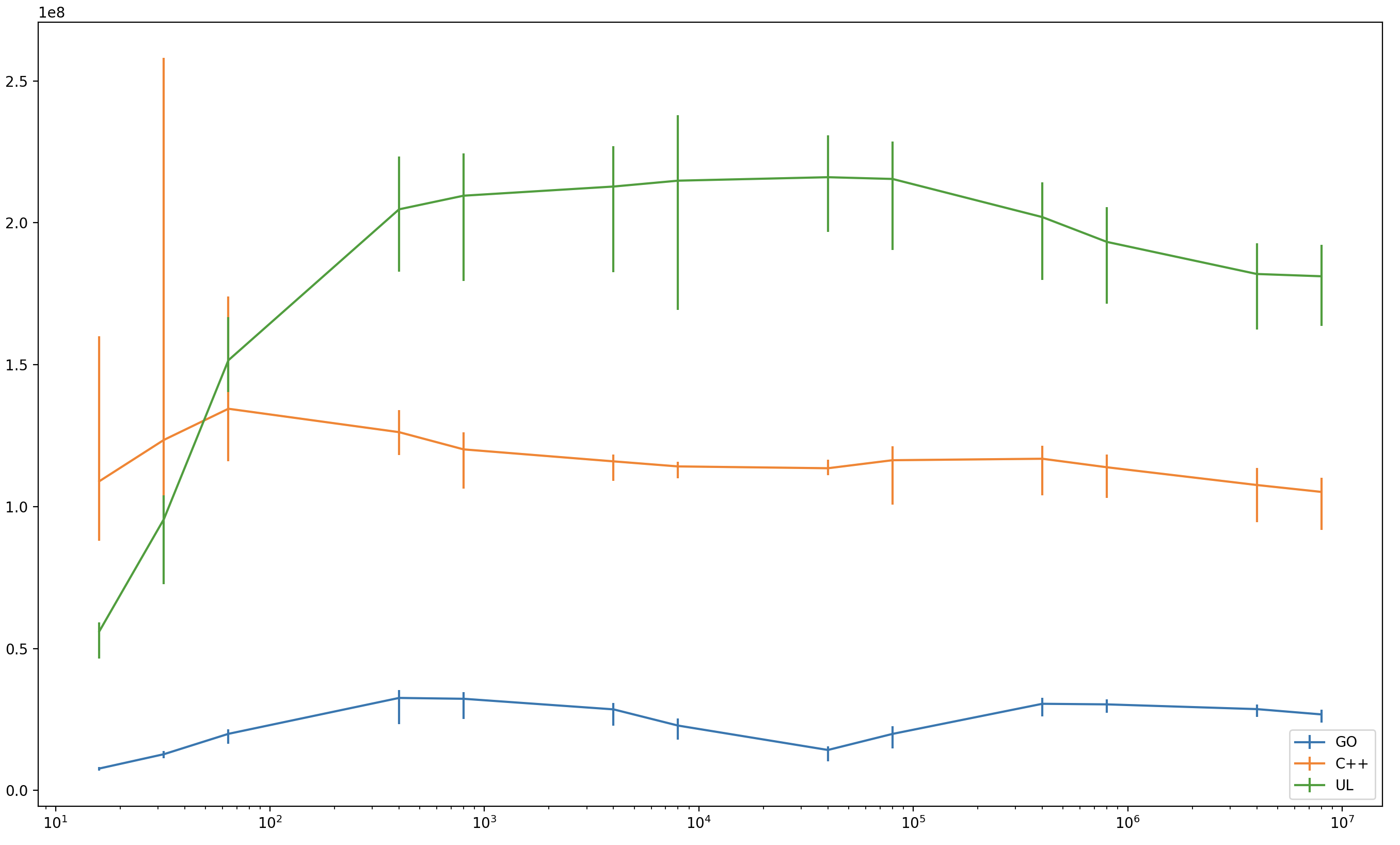
Results are amazing: usched actually beats compiler-assisted C++ coroutines by a large margin. The horizontal axis is the number of coroutines in the test (logarithmic) and the vertical axis is coroutine wakeup-wait operations per second (1 == 1e8 op/sec).

	16	32	64	400	800	4000	8000	40000	80000	400000	800000	4M	8M
GO	0.077	0.127	0.199	0.326	0.323	0.285	0.228	0.142	0.199	0.305	0.303	0.286	0.268
C++	1.089	1.234	1.344	1.262	1.201	1.159	1.141	1.135	1.163	1.168	1.138	1.076	1.051
UL	0.560	0.955	1.515	2.047	2.095	2.127	2.148	2.160	2.154	2.020	1.932	1.819	1.811

I only kept the most efficient implementation from every competing class: C++ for stackless, GO for stackful and usched for stackswap. See the full results in results.darwin

Generating Catalan numbers.

Enumerate all binary trees with N nodes, C++20 way:   

#include <memory>
#include <string>
#include <cassert>
#include <iostream>
#include <coroutine>
#include <cppcoro/generator.hpp>

struct tnode;
using tree = std::shared_ptr<tnode>;
struct tnode {
	tree left;
	tree right;
	tnode() {};
	tnode(tree l, tree r) : left(l), right(r) {}
};

auto print(tree t) -> std::string {
	return  t ? (std::string{"["} + print(t->left) + " "
		     + print(t->right) + "]") : "*";
}

cppcoro::generator<tree> gen(int n) {
	if (n == 0) {
		co_yield nullptr;
	} else {
		for (int i = 0; i < n; ++i) {
			for (auto left : gen(i)) {
				for (auto right : gen(n - i - 1)) {
					co_yield tree(new tnode(left, right));
				}
			}
		}
	}
}

int main(int argc, char **argv) {
	for (auto t : gen(std::atoi(argv[1]))) {
		std::cout << print(t) << std::endl;
	}
}

Source: gen.cpp. 

To generate Catalan numbers, do:

$ for i in $(seq 0 1000000) ;do ./gen $i | wc -l ;done
       1
       1
       2
       5
      14
      42
     132
     429
    1430
    4862
   16796
   58786
  208012
  742900

A Python: it's dictionaries all the way down.

def drill():
    return defaultdict(drill)

usched: stackswap coroutines, neither stackful nor stackless

[Please read the update.]

This repository (https://github.com/nikitadanilov/usched) contains a simple experimental implementation of coroutines alternative to well-known "stackless" and "stackful" methods.

The term "coroutine" gradually grew to mean a mechanism where a computation, which in this context means a chain of nested function calls, can "block" or "yield" so that the top-most caller can proceed and the computation can later be resumed at the blocking point with the chain of intermediate function activation frames preserved.

Prototypical uses of coroutines are lightweight support for potentially blocking operations (user interaction, IO, networking) and generators, which produce multiple values (see same fringe problem).

There are two common coroutine implementation methods:

• a stackful coroutine runs on a separate stack. When a stackful coroutine blocks, it performs a usual context switch. Historically "coroutines" meant stackful coroutines. Stackful coroutines are basically little more than usual threads, and so they can be kernel (supported by the operating system) or user-space (implemented by a user-space library, also known as green threads), preemptive or cooperative.

• a stackless coroutine does not use any stack when blocked. In a typical implementation instead of using a normal function activation frame on the stack, the coroutine uses a special activation frame allocated in the heap so that it can outlive its caller. Using heap-allocated frame to store all local variable lends itself naturally to compiler support, but some people are known to implement stackless coroutines manually via a combination of pre-processing, library and tricks much worse than Duff's device.

Stackful and stateless are by no means the only possibilities. One of the earliest languages to feature generators CLU (distribution) ran generators on the caller's stack.

usched is in some sense intermediate between stackful and stackless: its coroutines do not use stack when blocked, nor do they allocate individual activation frames in the heap.

The following is copied with some abbreviations from usched.c.

Overview

usched: A simple dispatcher for cooperative user-space threads.

A typical implementation of user-space threads allocates a separate stack for each thread when the thread is created and then dispatches threads (as decided by the scheduler) through some context switching mechanism, for example, longjmp().

In usched all threads (represented by struct ustack) are executed on the same "native" stack. When a thread is about to block (usched_block()), a memory buffer for the stack used by this thread is allocated and the stack is copied to the buffer. After that the part of the stack used by the blocking thread is discarded (by longjmp()-ing to the base of the stack) and a new thread is selected. The stack of the selected thread is restored from its buffer and the thread is resumed by longjmp()-ing to the usched_block() that blocked it.

The focus of this implementation is simplicity: the total size of usched.[ch] is less than 120LOC, as measured by SLOCCount.

Advantages:

• no need to allocate maximal possible stack at thread initialisation: stack buffer is allocated as needed. It is also possible to free the buffer when the thread is resumed (not currently implemented);

• thread that doesn't block has 0 overhead: it is executed as a native function call (through a function pointer) without any context switching;

• because the threads are executed on the stack of the same native underlying thread, native synchronisation primitives (mutices, etc.) work, although the threads share underlying TLS. Of course one cannot use native primitives to synchronise between usched threads running on the same native thread.

Disadvantages:

• stack copying introduces overhead (memcpy()) in each context switch;

• because stacks are moved around, addresses on a thread stack are only valid while the thread is running. This invalidates certain common programming idioms: other threads and heap cannot store pointers to the stacks, at least to the stacks of the blocked threads. Note that Go language, and probably other run-times, maintains a similar invariant.

Usage

usched is only a dispatcher and not a scheduler: it blocks and resumes threads but

• it does not keep track of threads (specifically allocation and freeing of struct ustack instances is done elsewhere),

• it implements no scheduling policies.

These things are left to the user, together with stack buffers allocation and freeing. The user supplies 3 call-backs:

• usched::s_next(): the scheduling function. This call-backs returns the next thread to execute. This can be either a new (never before executed) thread initialised with ustack_init(), or it can be a blocked thread. The user must keep track of blocked and runnable threads, presumably by providing wrappers to ustack_init() and ustack_block() that would record thread state changes. It is up to usched::s_next() to block and wait for events if there are no runnable threads and all threads are waiting for something;

• usched::s_alloc(): allocates new stack buffer of at least the specified size. The user have full control over stack buffer allocation. It is possible to pre-allocate the buffer when the thread is initialised (reducing the cost of usched_block()), it is possible to cache buffers, etc.;

• usched::s_free(): frees the previously allocated stack buffer.

rr.h and rr.c provide a simple "round-robin" scheduler implementing all the call-backs. Use it carefully, it was only tested with rmain.c benchmark.

Pictures!

The following diagrams show stack management by usched. The stack grows from right to left.

At the entrance to the dispatcher loop. usched_run(S):

                                                usched_run()
----------------------------------------------+--------------+-------+
                                              | buf | anchor |  ...  |
----------------------------------------------+--------------+-------+
                                              ^
                                              |
                                              sp = S->s_buf

A new (never before executed) thread U is selected by S->s_next(), launch() calls the thread startup function U->u_f():

                               U->u_f() launch() usched_run()
 -----------------------------+---------+-----+--------------+-------+
                              |         | pad | buf | anchor |  ...  |
 -----------------------------+---------+-----+--------------+-------+
                              ^         ^
                              |         |
                              sp        U->u_bottom

The thread executes as usual on the stack, until it blocks by calling usched_block():

    usched_block()       bar() U->u_f() launch() usched_run()
 ----------+------+-----+-----+---------+-----+--------------+-------+
           | here | ... |     |         | pad | buf | anchor |  ...  |
 ----------+------+-----+-----+---------+-----+--------------+-------+
      ^    ^                            ^
      |    +-- sp = U->u_cont           |
      |                                 U->u_bottom
      U->u_top

The stack from U->u_top to U->u_bottom is copied into the stack buffer U->u_stack, and control returns to usched_run() by longjmp(S->s_buf):

                                                usched_run()
----------------------------------------------+--------------+-------+
                                              | buf | anchor |  ...  |
----------------------------------------------+--------------+-------+
                                              ^
                                              |
                                              sp = S->s_buf

Next, suppose S->s_next() selects a previously blocked thread V ready to be resumed. usched_run() calls cont(V).

                                        cont()  usched_run()
----------------------------------------+-----+--------------+-------+
                                        |     | buf | anchor |  ...  |
----------------------------------------+-----+--------------+-------+
                                        ^
                                        |
                                        sp




cont() copies the stack from the buffer to [V->u_top, V->u_bottom] range. It's important that this memcpy() operation does not overwrite cont()'s own stack frame, this is why pad[] array is needed in launch(): it advances V->u_bottom and gives cont() some space to operate.

  usched_block()       foo() V->u_f()   cont()  usched_run()
---------+------+-----+-----+--------+--+-----+--------------+-------+
         | here | ... |     |        |  |     | buf | anchor |  ...  |
---------+------+-----+-----+--------+--+-----+--------------+-------+
    ^    ^                           ^  ^
    |    +-- V->u_cont               |  +-- sp
    |                                |
    V->u_top                         V->u_bottom

Then cont() longjmp()-s to V->u_cont, restoring V execution context:

  usched_block()       foo() V->u_f()   cont()  usched_run()
---------+------+-----+-----+--------+--+-----+--------------+-------+
         | here | ... |     |        |  |     | buf | anchor |  ...  |
---------+------+-----+-----+--------+--+-----+--------------+-------+
         ^
         +-- sp = V->u_cont




V continues its execution as if it returned from usched_block().

Multiprocessing

By design, a single instance of struct usched cannot take advantage of multiple processors, because all its threads are executing within a single native thread. Multiple instances of struct usched can co-exist within a single process address space, but a ustack thread created for one instance cannot be migrated to another. One possible strategy to add support for multiple processors is to create multiple instances of struct usched and schedule them (that is, schedule the threads running respective usched_run()-s) to processors via pthread_setaffinity_np() or similar. See rr.c for a simplistic implementation.

Current limitations

• the stack is assumed to grow toward lower addresses. This is easy to fix, if necessary;

• the implementation is not signal-safe. Fixing this can be as easy as replacing *jmp() calls with their sig*jmp() counterparts. At the moment signal-based code, like gperf -lprofiler library, would most likely crash usched;

• usched.c must be compiled without optimisations and with -fno-stack-protector option (gcc);

• usched threads are cooperative: a thread will continue to run until it completes of blocks. Adding preemption (via signal-based timers) is relatively easy, the actual preemption decision will be relegated to the external "scheduler" via a new usched::s_preempt() call-back invoked from a signal handler.

Notes

Midori seems to use a similar method: a coroutine (called activity there) starts on the native stack. If it needs to block, frames are allocated in the heap (this requires compiler support) and filled in from the stack, the coroutine runs in these heap-allocated frames when resumed.

Benchmarks

usched was benchmarked against a few stackful (go, pthreads) and stackless (rust, c++ coroutines) implementations. A couple of caveats:

• all benchmarking in general is subject to the reservations voiced by Hippocrates and usually translated (with the complete reversal of the meaning) as ars longa, vita brevis, which means: "the art [of doctor or tester] takes long time to learn, but the life of a student is brief, symptoms are vague, chances of success are doubtful".

• the author is much less than fluent with all the languages and frameworks used in the benchmarking. It is possible that some of the benchmarking code is inefficient or just outright wrong. Any comments are appreciated.

The benchmark tries to measure the efficiency of coroutine switching. It creates R cycles, N coroutines each. Each cycle performs M rounds, where each round consists of sending a message across the cycle: a particular coroutine (selected depending on the round number) sends the message to its right neighbour, all other coroutines relay the message received from the left to the right, the round completes when the originator receives the message after it passed through the entire cycle.

If N == 2, the benchmark is R pairs of processes, ping-ponging M messages within each pair.

Some benchmarks support two additional parameters: D (additional space in bytes, artificially consumed by each coroutine in its frame) and P (the number of native threads used to schedule the coroutines.

The benchmark creates N*R coroutines and sends a total of N*R*M messages, the latter being proportional to the number of coroutine switches.

bench.sh runs all implementations with the same N, R and M parameters. graph.py plots the results.

• POSIX. Source: pmain.c, binary: pmain. Pthreads-based stackful implementation in C. Uses default thread attributes. pmain.c also contains emulation of unnamed POSIX semaphores for Darwin. Plot label: "P". This benchmarks crashes with "pmain: pthread_create: Resource temporarily unavailable" for large values of N*R.

• Go. Source: gmain.go, binary: gmain. The code is straightforward (it was a pleasure to write). D is supported via runtime.GOMAXPROCS(). "GO1T" are the results for a single native thread, "GO" are the results without the restriction on the number of threads.

• Rust. Source: cycle/src/main.rs, binary: cycle/target/release/cycle. Stackless implementation using Rust builtin async/.await. Label: "R". It is single-threaded (I haven't figured out how to distribute coroutines to multiple executors), so should be compared with GO1T, C++1T and U1T. Instead of fighting with the Rust borrow checker, I used "unsafe" and shared data-structures between multiple coroutines much like other benchmarks do.

• C++. Source: c++main.cpp, binary: c++main. The current state of coroutine support in C++ is unclear. Is everybody supposed to directly use <coroutine> interfaces or one of the mutually incompatible libraries that provide easier to use interfaces on top of <coroutine>? This benchmark uses Lewis Baker's cppcoro, (Andreas Buhr's fork). Labels: "C++" and "C++1T" (for single-threaded results).

• usched. Source: rmain.c, binary: rmain. Based on usched.[ch] and rr.[ch] This is our main interest, so we test a few combinations of parameters.

  • Label: "U": the default configuration, round-robin scheduler over 16 native threads,
  • "U1K": 1000 bytes of additional stack space for each coroutine
  • "U10K": 10000 bytes,
  • "U1T": round-robin over 1 native thread,
  • "U1TS": round-robin over 1 native thread with pthread locking in rr.c compiled out (-DSINGLE_THREAD compilation option, a separate binary rmain.1t).
  • Update "UL": uses "local" scheduler ll.c. All coroutines within a cycle are assigned to the same native thread so that scheduling between them require no locking. This demonstrates very high throughput (comparable to C++), but unfortunately I do not have time right now to re-do all the measurements consistently. Binary: lmain.

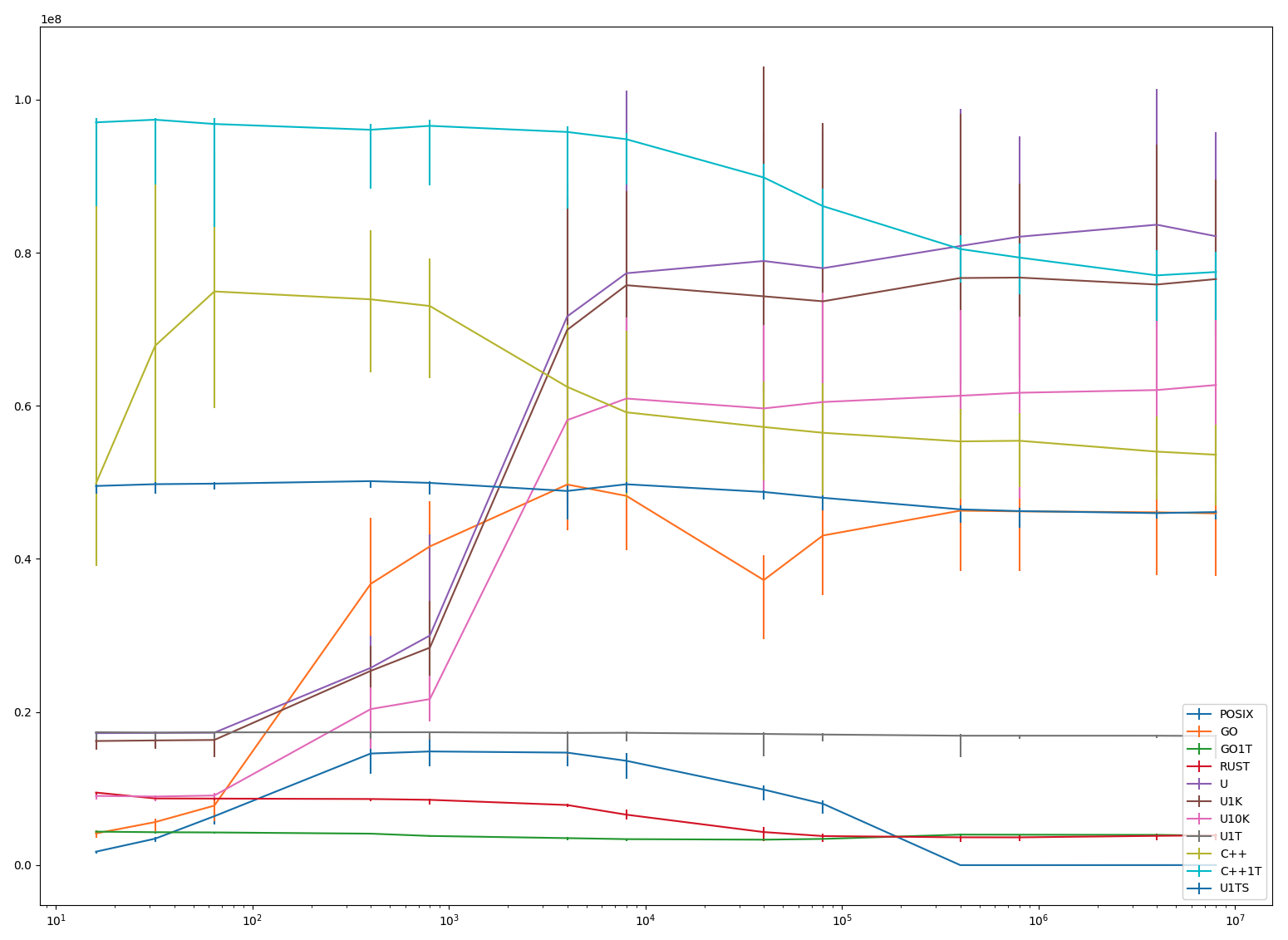
bench.sh runs all benchmarks with N == 2 (message ping-pong) and N == 8. Raw results are in results.linux. In the graphs, the horizontal axis is the number of coroutines (N*R, logarithmic) and the vertical axis is the operations (N*R*M) per second

Environment: Linux VM, 16 processors, 16GB of memory. Kernel: 4.18.0 (Rocky Linux).

	16	32	64	400	800	4000	8000	40000	80000	400000	800000	4000000	8000000
POSIX	1.76	3.46	6.39	14.58	14.85	14.70	13.63	9.87	8.02	0.00	0.00	0.00	0.01
GO	4.14	5.62	7.77	36.74	41.64	49.72	48.24	37.24	43.06	46.31	46.22	46.09	45.95
GO1T	4.38	4.30	4.27	4.11	3.81	3.53	3.40	3.33	3.43	3.99	3.98	3.95	3.86
RUST	9.48	8.71	8.69	8.64	8.53	7.85	6.59	4.32	3.80	3.63	3.63	3.83	3.90
U	17.24	17.27	17.30	25.77	29.99	71.68	77.32	78.92	77.98	80.88	82.09	83.66	82.15
U1K	16.21	16.29	16.35	25.38	28.41	69.92	75.76	74.31	73.65	76.69	76.75	75.84	76.56
U10K	9.04	8.96	9.09	20.38	21.69	58.13	60.95	59.66	60.50	61.32	61.71	62.06	62.72
U1T	17.37	17.31	17.35	17.35	17.36	17.27	17.29	17.14	17.06	16.91	16.91	16.91	16.87
C++	49.87	67.85	74.94	73.91	73.04	62.48	59.15	57.23	56.48	55.35	55.44	54.02	53.61
C++1T	97.03	97.38	96.82	96.06	96.58	95.78	94.83	89.83	86.09	80.48	79.37	77.04	77.48
U1TS	49.53	49.76	49.83	50.16	49.93	48.88	49.75	48.75	47.99	46.48	46.25	45.99	46.12
UL	76.03	116.63	160.72	169.74	169.99	171.57	170.32	165.82	169.43	174.32	171.55	169.48	170.04

(N == 8) A few notes:

• As mentioned above, pthreads-based solution crashes with around 50K threads.

• Most single-threaded versions ("GO1T", "R" and "U1T") are stable as corpse's body temperature. Rust cools off completely at about 500K coroutines. Single-threaded C++ ("C++1T") on the other hand is the most performant solution for almost the entire range of measurement, it is only for coroutine counts higher than 500K when "U" overtakes it.

• It is interesting that a very simple and unoptimised usched fares so well against heavily optimized C++ and Go run-times. (Again, see the reservations about the benchmarking.)

• Rust is disappointing: one would hope to get better results from a rich type combined with compiler support.

	4	8	16	100	200	1000	2000	10000	20000	100000	200000	1000000	2000000
POSIX	0.56	0.97	1.84	6.36	6.88	7.78	7.82	7.58	7.15	5.34	0.00	0.00	0.00
GO	7.40	11.03	19.23	40.44	45.79	51.81	52.87	52.77	53.15	53.62	53.22	55.77	56.82
GO1T	4.54	4.55	4.53	4.53	4.53	4.52	4.52	4.50	4.47	4.36	4.31	4.26	4.26
RUST	5.68	5.75	5.75	4.74	4.74	4.62	4.46	4.13	3.70	2.81	2.77	2.76	2.73
U	11.22	11.27	11.26	11.30	7.91	24.66	38.72	35.67	40.60	41.18	42.06	42.96	42.74
U1K	9.64	9.62	9.65	9.67	7.61	22.14	34.38	31.70	34.54	34.56	34.59	35.47	35.56
U10K	4.43	4.62	4.50	4.25	5.02	15.79	26.18	25.33	27.60	27.62	27.63	27.72	28.16
U1T	11.24	11.29	11.34	11.26	11.32	11.30	11.28	11.28	11.22	11.19	11.15	11.13	11.15
C++	46.33	46.30	63.38	114.30	117.05	114.12	111.36	101.32	100.13	84.30	78.53	72.77	71.00
C++1T	96.56	96.03	96.37	95.97	95.49	95.68	94.94	92.95	91.23	83.55	80.33	77.22	76.22
U1TS	19.59	19.66	19.80	19.87	19.89	19.86	19.82	19.72	19.66	19.51	19.45	19.33	19.37
UL	12.19	23.48	50.39	65.71	67.22	69.17	70.01	70.09	69.36	69.28	69.43	68.83	68.00

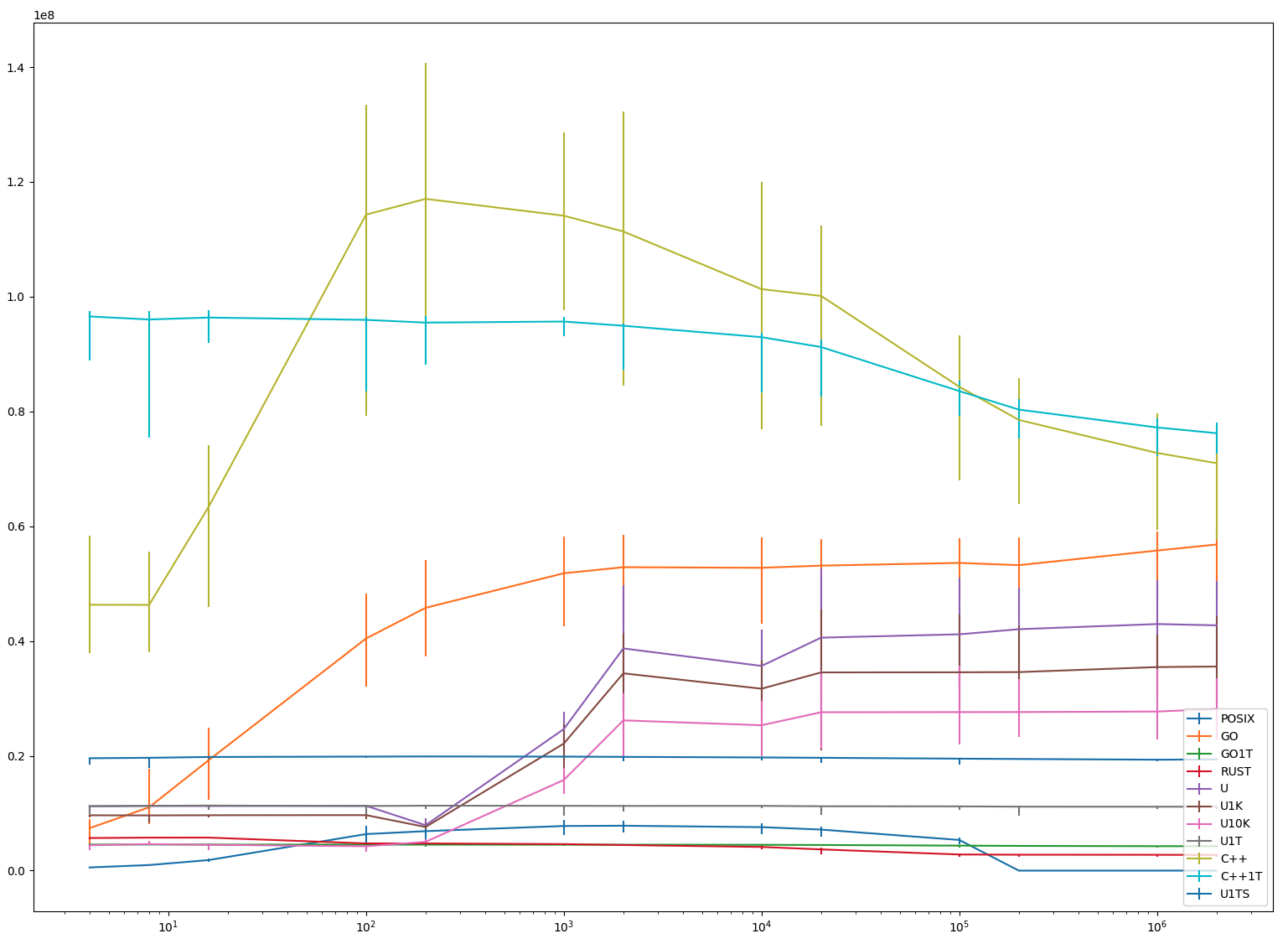
(N == 2)

• First, note that the scale is different on the vertical axis.

• Single-threaded benchmarks display roughly the same behaviour (exactly the same in "C++1T" case) as with N == 8.

• Go is somewhat better. Perhaps its scheduler is optimised for message ping-pong usual in channel-based concurrency models?

• usched variants are much worse (50% worse for "U") than N == 8.

• Rust is disappointing.

To reproduce:

$ # install libraries and everything, then...
$ make
$ while : ;do ./bench.sh | tee -a results; sleep 5 ;done # collect enough results, this might take long...
^C
$ grep -h '^ *[2N],' results | python3 graph.py c2.svg > c2-table.md # create plot for N == 2
$ grep -h '^ *[8N],' results | python3 graph.py c8.svg > c8-table.md # create plot for N == 8

Conclusion

Overall, the results are surprisingly good. The difference between "U1T" and "U1TS" indicates that the locking in rr.c affects performance significantly, and affects it even more with multiple native threads, when locks are contended across processors. I'll try to produce a more efficient (perhaps lockless) version of a scheduler as the next step.

3-lisp: an infinite tower of meta-circular interpreters.

Précis

3-lisp is a dialect of Lisp designed and implemented by Brian C. Smith as part of his PhD. thesis Procedural Reflection in Programming Languages (what this thesis refers to as "reflection" is nowadays more usually called "reification"). A 3-lisp program is conceptually executed by an interpreter written in 3-lisp that is itself executed by an interpreter written in 3-lisp and so on ad infinitum. This forms a (countably) infinite tower of meta-circular (v.i.) interpreters. reflective lambda is a function that is executed one tower level above its caller. Reflective lambdas provide a very general language extension mechanism.

The code is here.

Meta-circular interpreters

An interpreter is a program that executes programs written in some programming language.

A meta-circular interpreter is an interpreter for a programming language written in that language. Meta-circular interpreters can be used to clarify or define the semantics of the language by reducing the full language to a sub-language in which the interpreter is expressed. Historically, such definitional interpreters become popular within the functional programming community, see the classical Definitional interpreters for higher-order programming languages. Certain important techniques were classified and studied in the framework of meta-circular interpretation, for example, continuation passing style can be understood as a mechanism that makes meta-circular interpretation independent of the evaluation strategy: it allows an eager meta-language to interpret a lazy object language and vice versa. As a by-product, a continuation passing style interpreter is essentially a state machine and so can be implemented in hardware, see The Scheme-79 chip. Similarly, de-functionalisation of languages with higher-order functions obtains for them first-order interpreters. But meta-circular interpreters occur in imperative contexts too, for example, the usual proof of the Böhm–Jacopini theorem (interestingly, it was Corrado Böhm who first introduced meta-circular interpreters in his 1954 PhD. thesis) constructs for an Algol-like language a meta-circular interpreter expressed in some goto-less subset of the language and then specialises this interpreter for a particular program in the source language.

Given a language with a meta-circular interpreter, suppose that the language is extended with a mechanism to trap to the meta-level. For example, in a lisp-like language, that trap can be a new special form (reflect FORM) that directly executes (rather than interprets) FORM within the interpreter. Smith is mostly interested in reflective (i.e., reification) powers obtained this way, and it is clear that the meta-level trap provides a very general language extension method: one can add new primitives, data types, flow and sequencing control operators, etc. But if you try to add reflect to an existing LISP meta-circular interpreter (for example, see p. 13 of LISP 1.5 Programmers Manual) you'd hit a problem: FORM cannot be executed at the meta-level, because at this level it is not a form, but an S-expression.

Meta-interpreting machine code

To understand the nature of the problem, consider a very simple case: the object language is the machine language (or equivalently the assembly language) of some processor. Suppose that the interpreter for the machine code is written in (or, more realistically, compiled to) the same machine language. The interpreter maintains the state of the simulated processor that is, among other things registers and memory. Say, the object (interpreted) code can access a register, R0, then the interpreter has to keep the contents of this register somewhere, but typically not in its (interpreter's) R0. Similarly, a memory word visible to the interpreted code at an address ADDR is stored by the interpreter at some, generally different, address ADDR' (although, by applying the contractive mapping theorem and a lot of hand-waving one might argue that there will be at least one word stored at the same address at the object- and meta-levels). Suppose that the interpreted machine language has the usual sub-routine call-return instructions call ADDR and return and is extended with a new instruction reflect ADDR that forces the interpreter to call the sub-routine ADDR. At the very least the interpreter needs to convert ADDR to the matching ADDR'. This might not be enough because, for example, the object-level sub-routine ADDR might not be contiguous at the meta-level, i.e., it is not guaranteed that if ADDR maps to ADDR' then (ADDR + 1) maps (ADDR' + 1). This example demonstrates that a reflective interpreter needs a systematic and efficient way of converting or translating between object- and meta-level representations. If such a method is somehow provided, reflect is a very powerful mechanism: by modifying interpreter state and code it can add new instructions, addressing modes, condition bits, branch predictors, etc.

N-LISP for a suitable value of N

In his thesis Prof. Smith analyses what would it take to construct a dialect of LISP for which a faithful reflective meta-circular interpreter is possible. He starts by defining a formal model of computation with an (extremely) rigorous distinction between meta- and object- levels (and, hence, between use and mention). It is then determined that this model can not be satisfactorily applied to the traditional LISP (which is called 1-LISP in the thesis and is mostly based on Maclisp). The reason is that LISP's notion of evaluation conflates two operations: normalisation that operates within the level and reference that moves one level down. A dialect of LISP that consistently separates normalisation and reference is called 2-LISP (the then new Scheme is called LISP-1.75). Definition of 2-LISP occupies the bulk of the thesis, which the curious reader should consult for (exciting, believe me) details.

Once 2-LISP is constructed, adding the reflective capability to it is relatively straightforward. Meta-level trap takes the form of a special lambda expression:

(lambda reflect [ARGS ENV CONT] BODY)

When this lambda function is applied (at the object level), the body is directly executed (not interpreted) at the meta-level with ARGS bound to the meta-level representation of the actual parameters, ENV bound to the environment (basically, the list of identifiers and the values they are bound to) and CONT bound to the continuation. Environment and continuation together represent the 3-LISP interpreter state (much like registers and memory represent the machine language interpreter state), this representation goes all the way back to SECD machine, see The Mechanical Evaluation of Expressions.

Here is the fragment of 3-LISP meta-circular interpreter code that handles lambda reflect (together with "ordinary" lambda-s, denoted by lambda simple):

Implementation

It is of course not possible to run an infinite tower of interpreters directly.

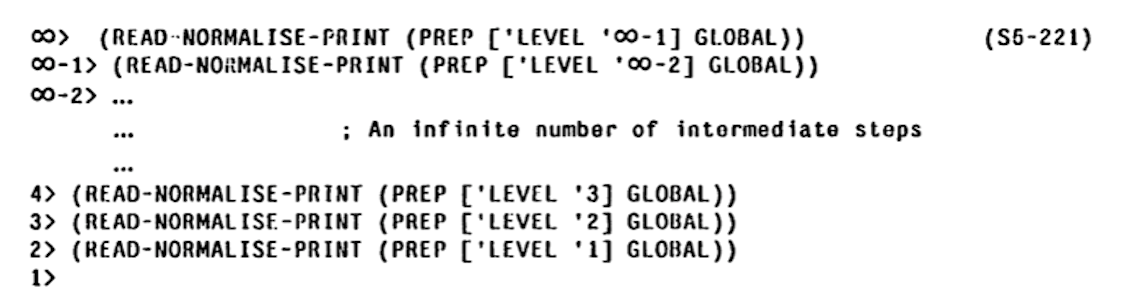
3-LISP implementation creates a meta-level on demand, when a reflective lambda is invoked. At that moment the state of the meta-level interpreter is synthesised (e.g., see make-c1 in the listing above). The implementation takes pain to detect when it can drop down to a lower level, which is not entirely simple because a reflective lambda can, instead of returning (that is, invoking the supplied continuation), run a potentially modified version of the read-eval-loop (called READ-NORMALISE-PRINT (see) in 3-LISP) which does not return. There is a lot of non-trivial machinery operating behind the scenes and though the implementation modestly proclaims itself EXTREMELY INEFFICIENT it is, in fact, remarkably fast.

Porting

I was unable to find a digital copy of the 3-LISP sources and so manually retyped the sources from the appendix of the thesis. The transcription in 3-lisp.lisp (2003 lines, 200K characters) preserves the original pagination and character set, see the comments at the top of the file. Transcription was mostly straightforward except for a few places where the PDF is illegible (for example, here) all of which fortunately are within comment blocks.

The sources are in CADR machine dialect of LISP, which, save for some minimal and no longer relevant details, is equivalent to Maclisp.

3-LISP implementation does not have its own parser or interpreter. Instead, it uses flexibility built in a lisp reader (see, readtables) to parse, interpret and even compile 3-LISP with a very small amount of additional code. Amazingly, this more than 40 years old code, which uses arcane features like readtable customisation, runs on a modern Common Lisp platform after a very small set of changes: some functions got renamed (CASEQ to CASE, *CATCH to CATCH, etc.), some functions are missing (MEMQ, FIXP), some signatures changed (TYPEP, BREAK, IF). See 3-lisp.cl for details.

Unfortunately, the port does not run on all modern Common Lisp implementations, because it relies on the proper support for backquotes across recursive reader invocations:

;;     Maclisp maintains backquote context across recursive parser
;;     invocations. For example in the expression (which happens within defun
;;     3-EXPAND-PAIR)
;;
;;         `\(PCONS ~,a ~,d)
;;
;;     the backquote is consumed by the top-level activation of READ. Backslash
;;     forces the switch to 3-lisp readtable and call to 3-READ to handle the
;;     rest of the expression. Within this 3-READ activation, the tilde forces
;;     switch back to L=READTABLE and a call to READ to handle ",a". In Maclisp,
;;     this second READ activation re-uses the backquote context established by
;;     the top-level READ activation. Of all Common Lisp implementations that I
;;     tried, only sbcl correctly handles this situation. Lisp Works and clisp
;;     complain about "comma outside of backquote". In clisp,
;;     clisp-2.49/src/io.d:read_top() explicitly binds BACKQUOTE-LEVEL to nil.

Among Common Lisp implementations I tried, only sbcl supports it properly. After reading Common Lisp Hyperspec, I believe that it is Maclisp and sbcl that implement the specification correctly and other implementations are faulty.

Conclusion

Procedural Reflection in Programming Languages is, in spite of its age, a very interesting read. Not only does it contain an implementation of a refreshingly new and bold idea (it is not even immediately obvious that infinite reflective towers can at all be implemented, not to say with any reasonable degree of efficiency), it is based on an interplay between mathematics and programming: the model of computation is proposed and afterward implemented in 3-LISP. Because the model is implemented in an actual running program, it has to be specified with extreme precision (which would make Tarski and Łukasiewicz tremble), and any execution of the 3-LISP interpreter validates the model.

Treadmill

Treadmill is a "real-time" in-place garbage collection algorithm designed by H. Baker [0]. It is simple, elegant, efficient and surprisingly little known. Speaking of which, Mr. Baker's Wikipedia page rivals one for an obscure Roman decadent poet in scarcity of information.

The general situation of garbage collection is that there is a program (called a mutator in this case) that allocates objects (that will also be called nodes) in a heap, which is a pool of memory managed by the garbage collector. The mutator can update objects to point to other earlier allocated objects so that objects form a graph, possibly with cycles. The mutator can store pointers to objects in some locations outside of the heap, for example in the stack or in the registers. These locations are called roots.

The mutator allocates objects, but does not frees them explicitly. It is the job of the garbage collector to return unreachable objects, that is, the objects that can not be reached by following pointers from the roots, back to the allocation pool.

It is assumed that the collector, by looking at an object, can identify all pointers to the heap stored in the object and that the collector knows all the roots. If either of these assumptions does not hold, one needs a conservative collector that can be implemented as a library for an uncooperative compiler and run-time (e.g., Boehm garbage collector for C and C++).

The earliest garbage collectors were part of Lisp run-time. Lisp programs tend to allocate a large number of cons cells and organise them in complex structures with cycles and sub-structure sharing. In fact, some of the Lisp Machines had garbage collection implemented in hardware and allocated everything including stack frames and binding environments in the heap. Even processor instructions were stored as cons cells in the heap.

To allocate a new object, the mutator calls alloc(). Treadmill is "real-time" because the cost of alloc() in terms of processor cycles is independent of the number of allocated objects and the total size of the heap, in other words, alloc() is O(1) and this constant cost is not high. This means garbage collection without "stop-the-world" pauses, at least as long as the mutator does not genuinely exhaust the heap with reachable objects. 

Treadmill is "in-place" because the address of an allocated object does not change. This is in contrast with copying garbage collectors that can move an object to a new place as part of the collection process (that implies some mechanism of updating the pointers to the moved object).

All existing garbage collection algorithms involve some form of scanning of allocated objects and this scanning is usually described in terms of colours assigned to objects. In the standard 3-colour scheme (introduced in [3] together with the term "mutator"), black objects have been completely scanned together with the objects they point to, gray objects have been scanned, but the objects they point to are not guaranteed to be scanned and white objects have not been scanned.  

For historical reasons, Baker's papers colour free (un-allocated) objects white and use black-gray-ecru instead of black-gray-white. We stick with ecru, at least to get a chance to learn a fancy word.

Consider the simplest case first:

• the heap has a fixed size;
• the mutator is single-threaded;
• allocated objects all have the same size (like cons cells).

(All these restrictions will be lifted eventually.)

The main idea of treadmill is that all objects in the heap are organised in a cyclic double-linked list, divided by 4 pointers into 4 segments:

Figure 0: treadmill

Allocation of new objects happens at free (clockwise), scan advances at scan (counterclockwise), still non-scanned objects are between bottom and top (the latter 2 terms, somewhat confusing for a cyclic list of objects, are re-used from an earlier paper [1], where a copying real-time garbage collector was introduced).

Remarkably, the entire description and the proof of correctness of Treadmill algorithm (and many other similar algorithms) depends on a single invariant:

Invariant: there are no pointers from black to ecru nodes.

That is, a black node can contain a pointer to another black node or to a gray node. A non-black (that is, gray or ecru) node can point to any allocated node: black, gray or ecru. An ecru node can be reached from a black node only through at least one intermediate gray node.

Let's for the time being postpone the explanation of why this invariant is important and instead discuss the usual 2 issues that any invariant introduces: how to establish it and how to maintain it.

Establishing is easy:

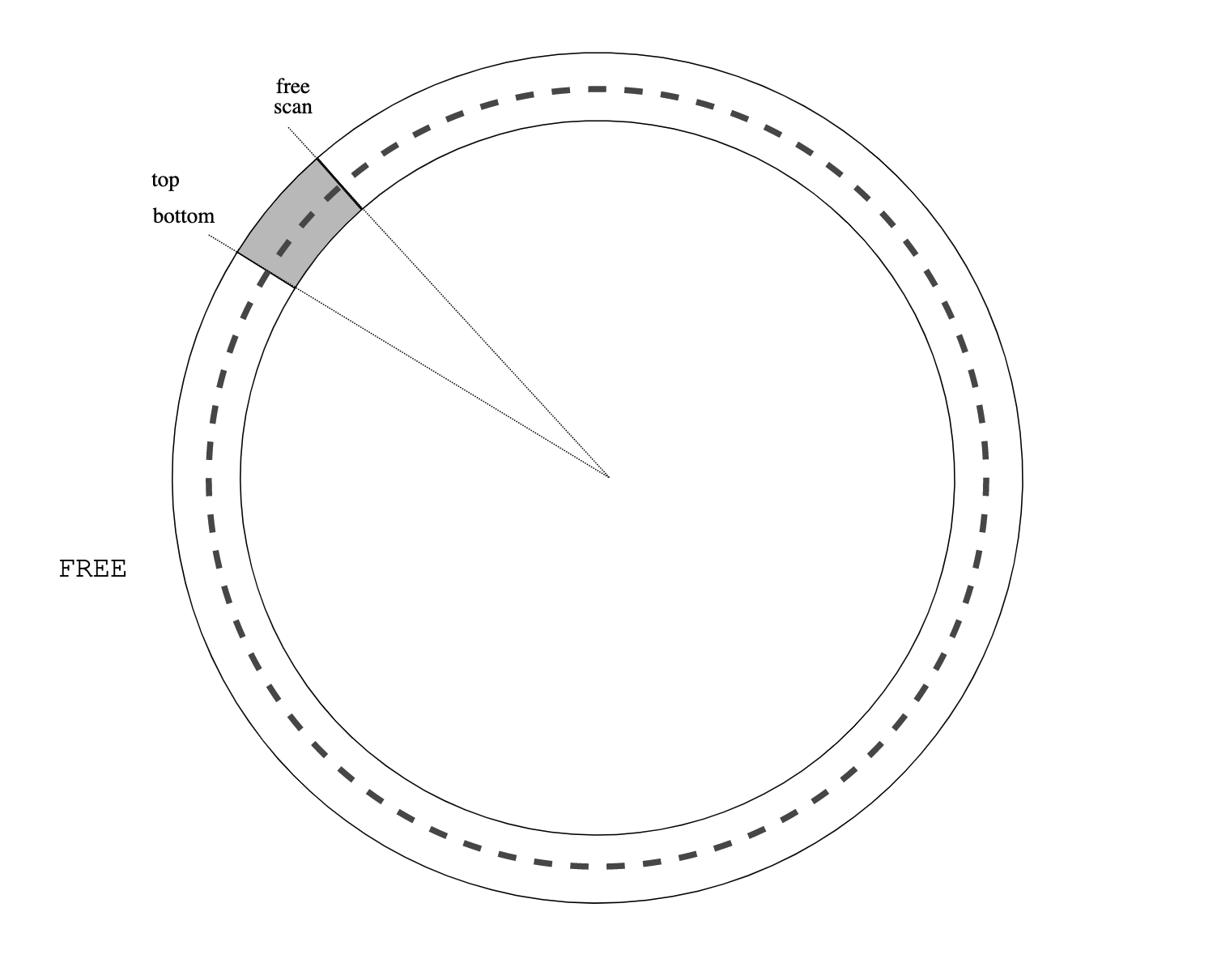Figure 1: initial heap state

In the initial state, all objects are un-allocated (white), except for the roots that are gray. The invariant is satisfied trivially because there are no black objects.

After some allocations by the mutator and scanning, the heap looks like the one in Figure 0. A call to alloc() advances free pointer clockwise, thus moving one object from FREE to SCANNED part of the heap. There is no need to update double-linked list pointers within the allocated object and, as we will see, there is no need to change the object colour. This makes the allocation fast path very quick: just a single pointer update: free := free.next.

Figure 2: alloc()

Allocation cannot violate the invariant, because the newly allocated object does not point to anything. In addition to calls to alloc() the mutator can read pointer fields from nodes it already reached and update fields of reachable nodes to point to other reachable nodes. There is no pointer arithmetic (otherwise a conservative collector is needed). A reachable node is either black, gray or ecru, so it seems, at the first sight, that the only way the mutator can violate the invariant is by setting a field in a black object to point to an ecru object. This is indeed the case with some collection algorithms (called "gray mutator algorithms" in [2]). Such algorithms use a write barrier, which is a special code inserted by the compiler before (or instead of) updating a pointer field. The simplest write barrier prevents a violation of the 3-colour invariant by graying the ecru target object if necessary:

writebarrier(obj, field, target) {
        obj.field := target;
        if black(obj) && ecru(target) {
                darken(target);
        }
}
darken(obj) { /* Make an ecru object gray. */
        assert ecru(obj);
        unlink(obj); /* Remove the object from the treadmill list. */
        link(top, obj); /* Put it back at the tail of the gray list. */
}

More sophisticated write barriers were studied that make use of the old value of obj.field or are integrated with virtual memory sub-system, see [2] for details. In our case, however, when the mutator reads a pointer field of an object, it effectively stores the read value in a register (or in a stack frame slot) and in Treadmill, registers can be black (Treadmill is a "black mutator algorithm"). That is, the mutator can violate the invariant simply by reading the pointer to an ecru object in a black register. To prevent this a read barrier is needed, executed on every read of a pointer field:

readbarrier(obj, field) {
        if ecru(obj) {
                darken(obj);
        }
        return obj.field;
}

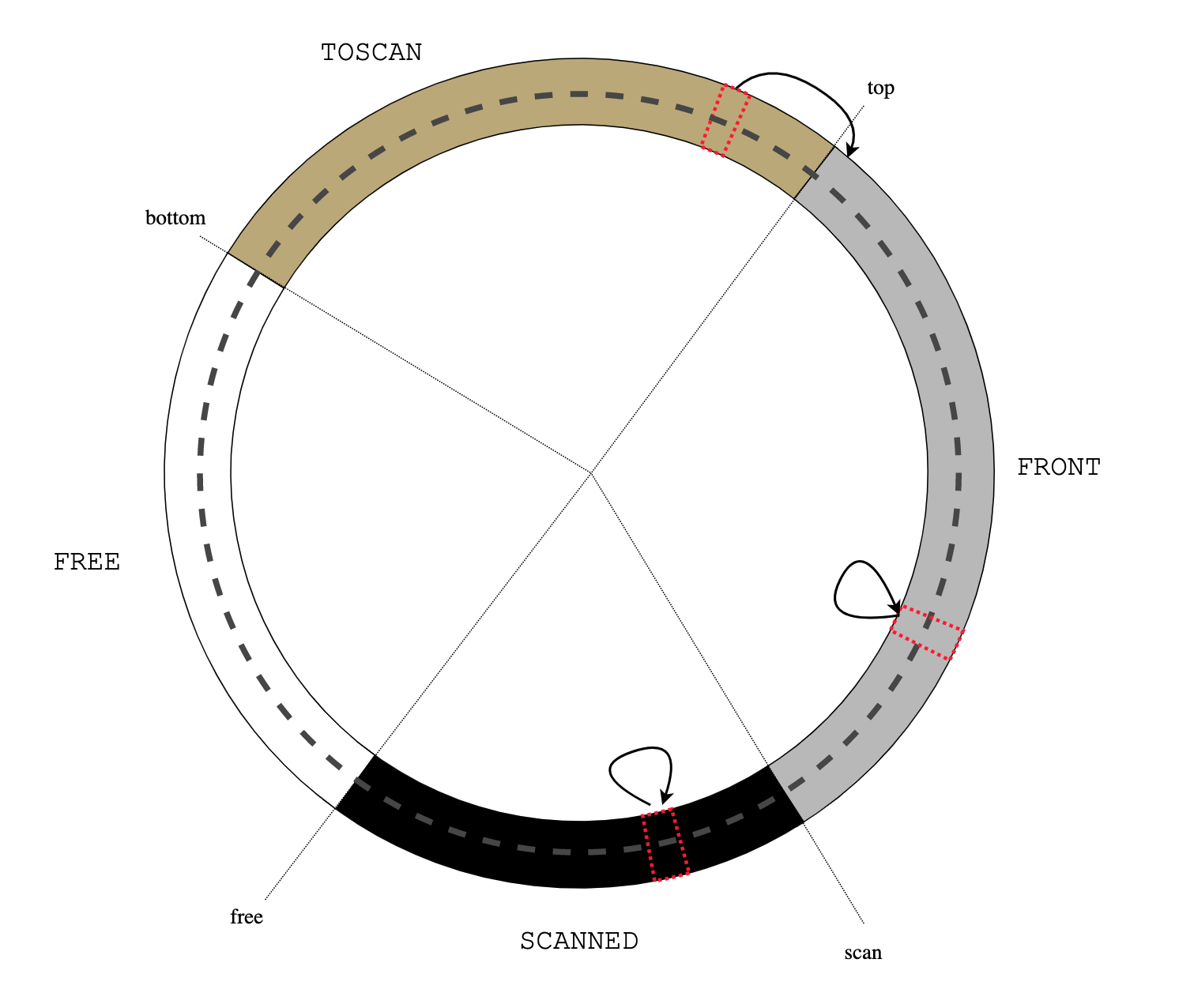
Figure 3: read barrier

When a black or gray object is read, the read barrier leaves it in place. When an ecru object is read, the barrier un-links the object from the treadmill list (effectively removing it from TOSCAN section) and re-links it to the treadmill either at top or at scan, thus making it gray. This barrier guarantees that the mutator cannot violate the invariant simply because the mutator never sees ecru objects (which are grayed by the barrier) and hence cannot store pointers to them anywhere. If the read barrier is present, the write barrier is not necessary.

That's how the invariant is established and maintained by the mutator. We still haven't discussed how the collector works and where these mysterious ecru objects appear from. The collector is very simple: it has a single entry point:

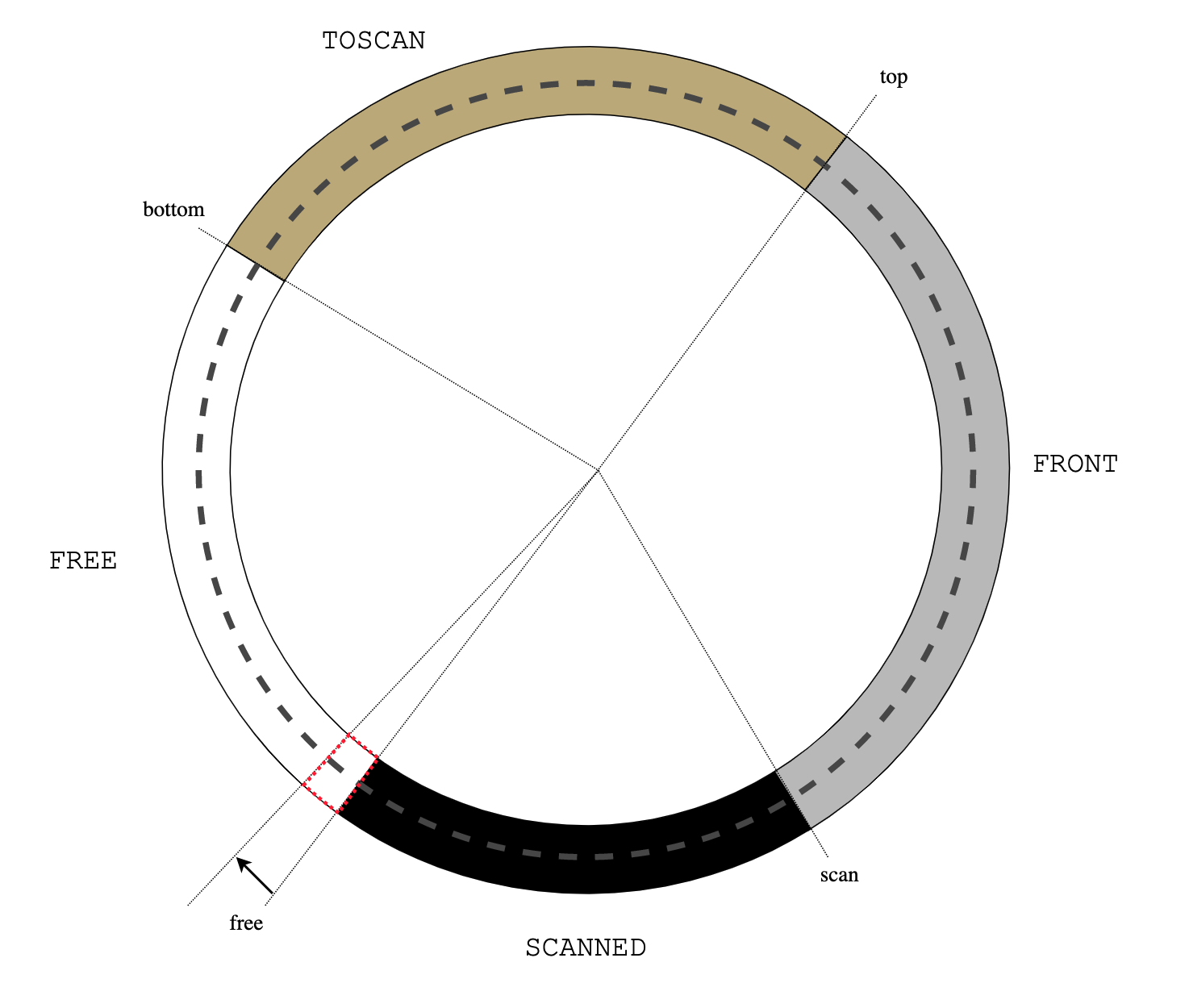
advance() { /* Scan the object pointed to by "scan". */
        for field in pointers(scan) {
                if ecru(scan.field) {
                        darken(scan.field);
                }
        }
        scan := scan.prev; /* Make it black. */
}

advance() takes the gray object pointed to by scan, which is the head of the FRONT list, and grays all ecru objects that this object points to. After that, scan is advanced (counterclockwise), effectively moving the scanned object into the SCANNED section and making it black.

Figure 4: advance()

It's not important for now how and when exactly advance() is called. What matters is that it blackens an object while preserving the invariant. 

Now comes the crucial part. An allocated object only darkens: the mutator (readbarrier()) and the collector (advance()) can gray an ecru object and advance() blackens a gray object. There is no way for a black object to turn gray or for a gray object to turn ecru. Hence, the total number of allocated non-black objects never increases. But advance() always blackens one object, which means that after some number of calls (interspersed with arbitrary mutator activity), advance() will run out of objects to process: the FRONT section will be empty and there will be no gray objects anymore:

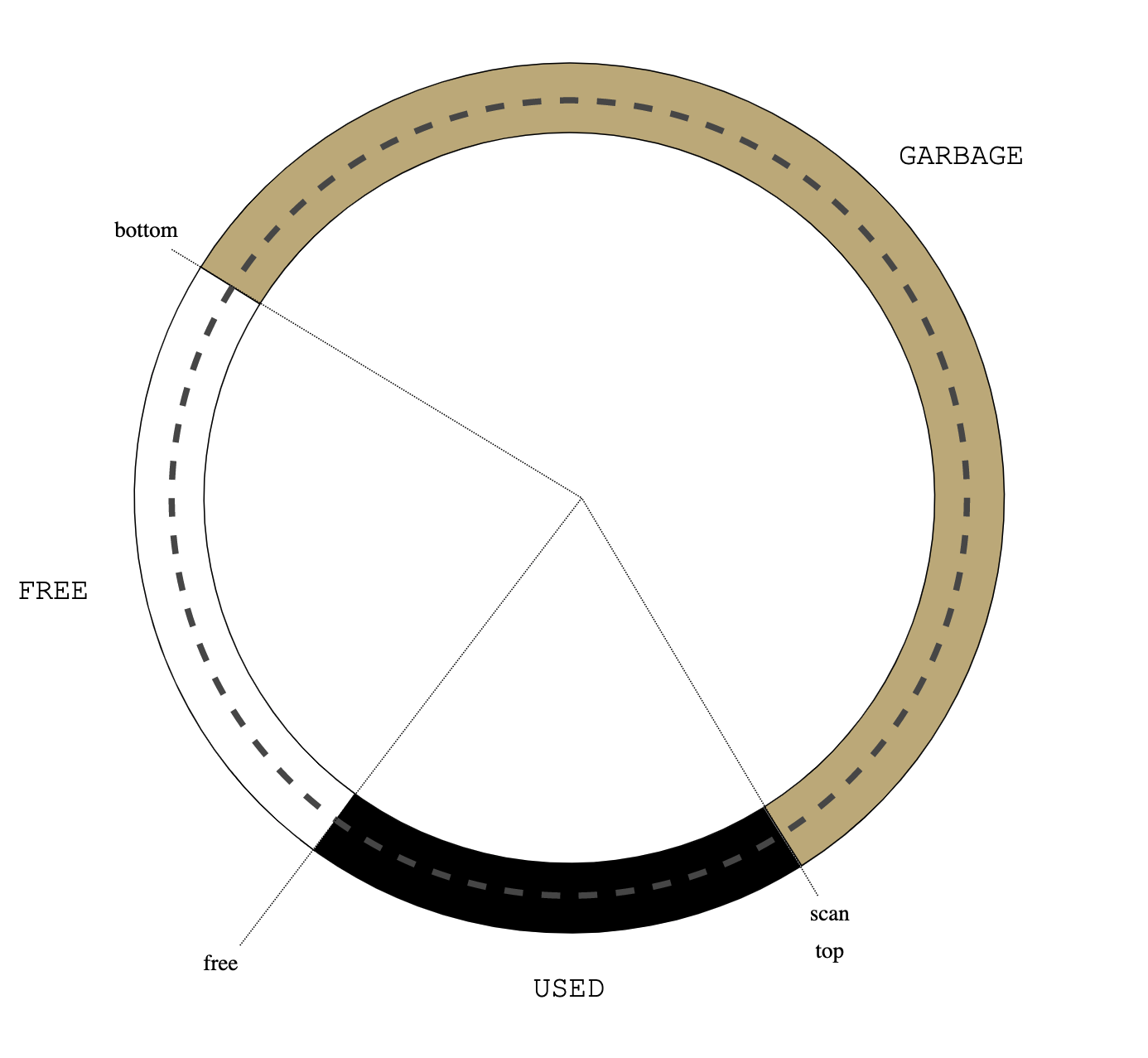Figure 5: no gray objects

All roots were originally gray and could only darken, so they are now black. And an ecru object is reachable from a black object only through a gray object, but there are no gray objects, so ecru objects are not reachable from roots—they are garbage. This completes the collection cycle and, in principle, it is possible to move all ecru objects to the FREE list at that point and start the next collection cycle. But we can do better. Instead of replenishing the FREE list, wait until all objects are allocated and the FREE list is empty:

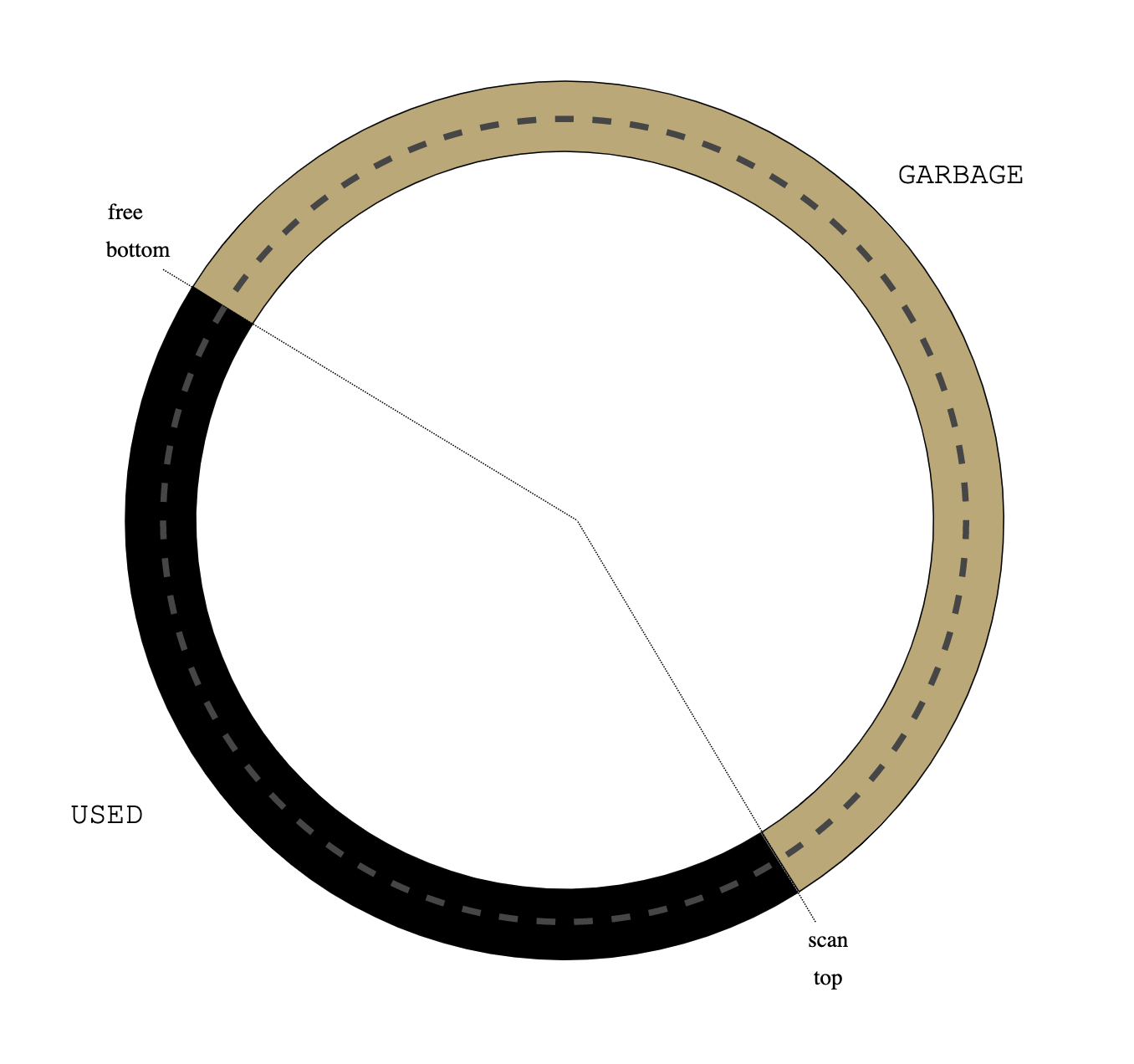Figure 6: neither gray nor white

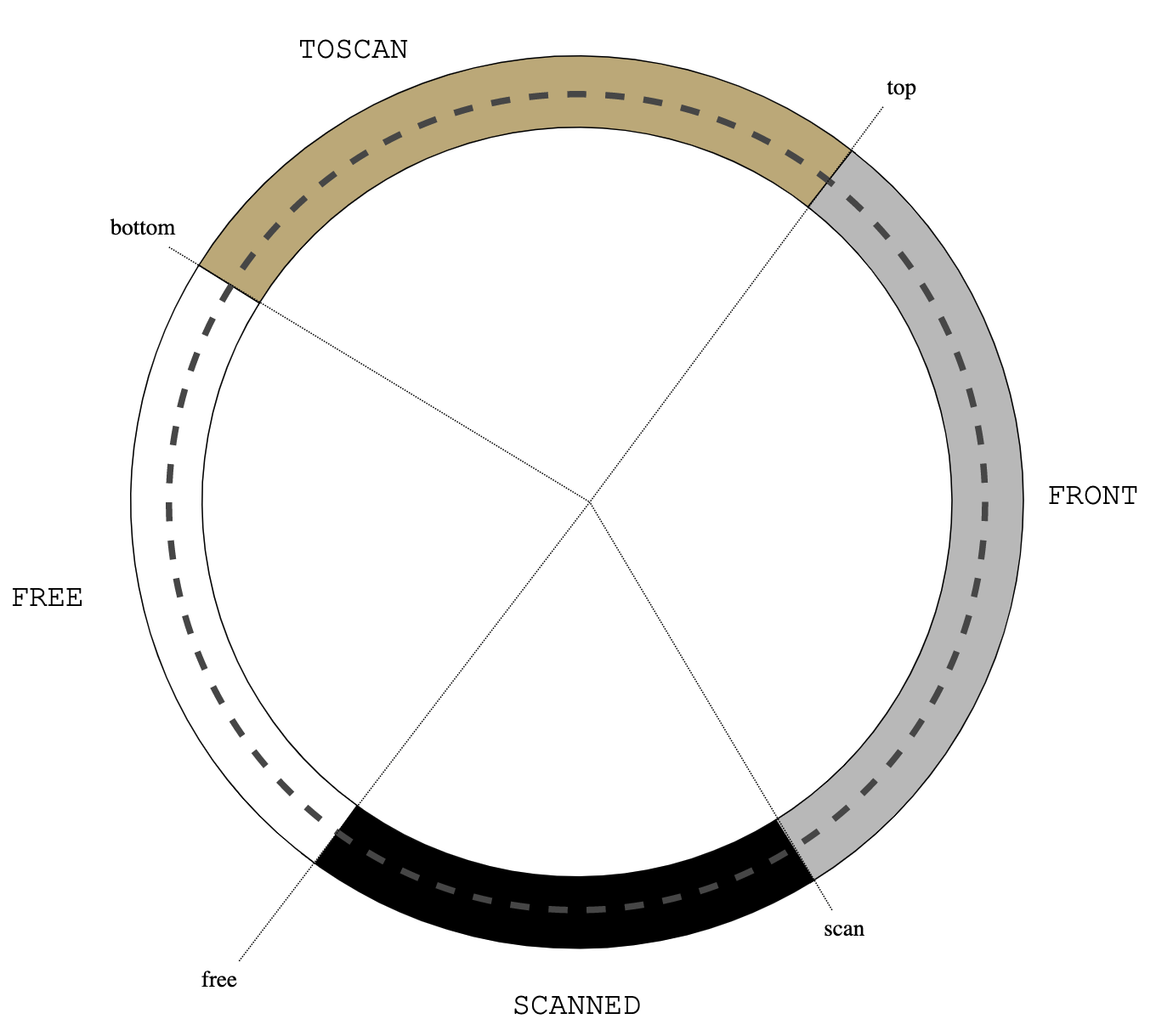
Only black and ecru objects remain. Flip them: swap top and bottom pointers and redefine colours: the old black objects are now ecru and the old ecru objects (remember they are garbage) are now white:

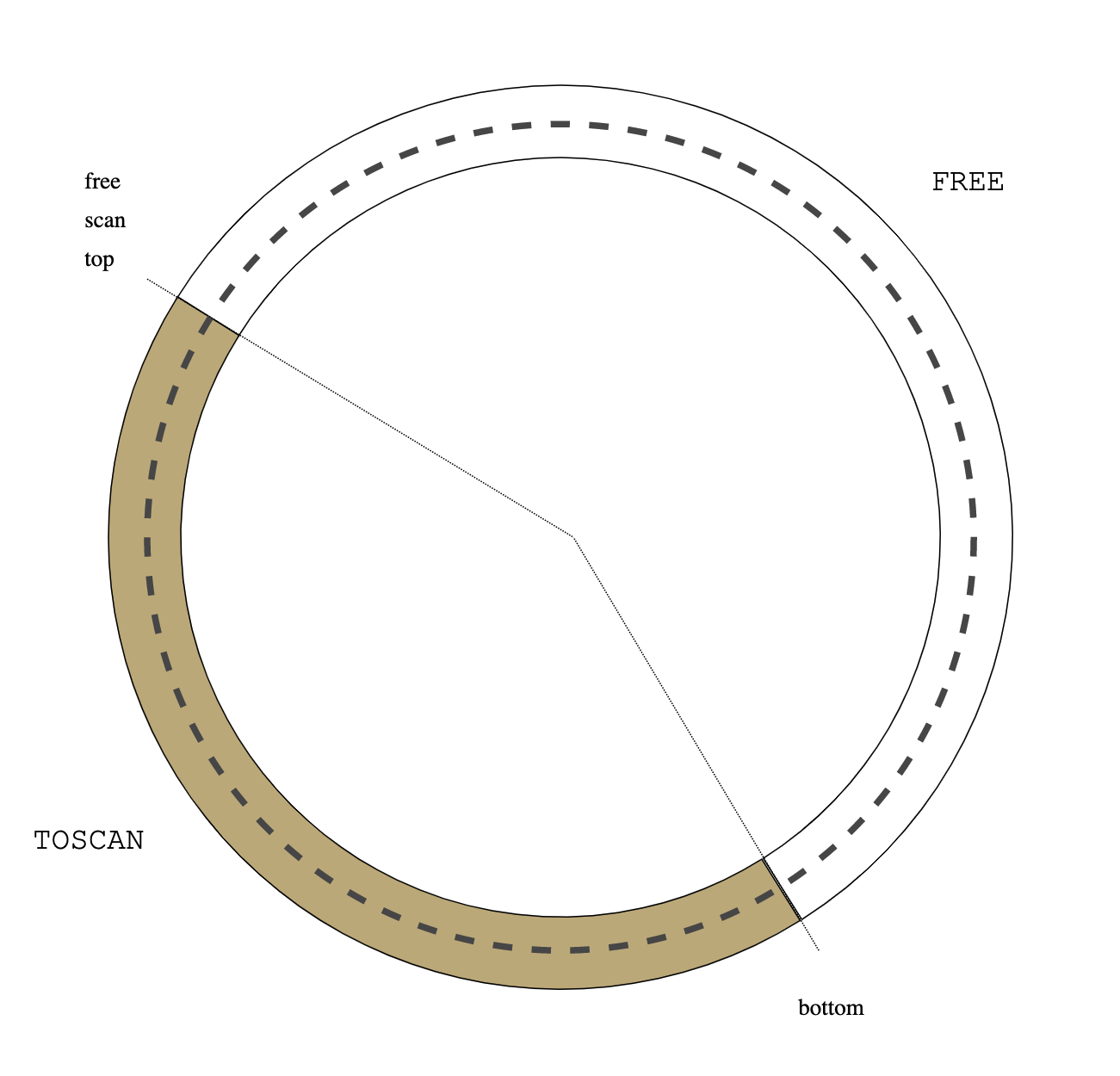Figure 7: flip

The next collection cycle starts: put the roots between top and scan so that they are the new FRONT:

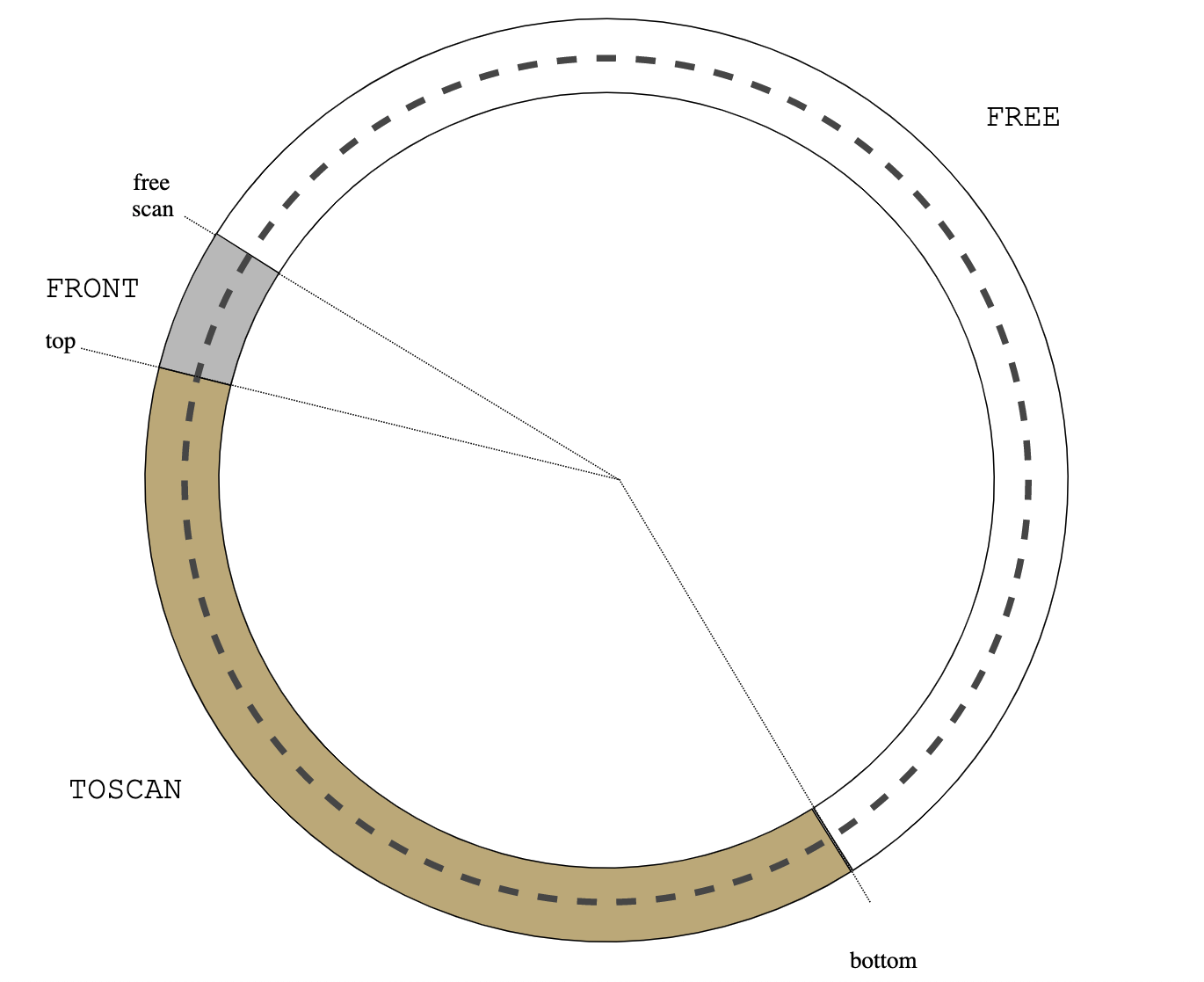Figure 8: new cycle

From this point alloc() and advance() can continue as before.

Note that alloc(), advance() and readbarrier() do not actually have to know object colour. They only should be able to tell an ecru (allocated) object from non-ecru, so 1 bit of information per object is required. By waiting until the FREE list is empty and re-defining colours Treadmill avoids the need to scan the objects and change their colours at the end of a collection cycle: it is completely O(1).

The last remaining bit of the puzzle is still lacking: how is it guaranteed that the collection is completed before the FREE list is empty? If the mutator runs out of free objects before the collection cycle is completed, then the only option is to force the cycle to completion by calling advance() repeatedly until there are no more gray objects and then flip, but that's a stop-the-world situation. The solution is to call advance() from within alloc() guaranteeing scan progress. Baker proved that if advance() is called k times for each alloc() call, then the algorithm never runs out of free objects, provided that the total heap size is at least R*(1 + 1/k) objects, where R is the number of reachable objects.

This completes the Treadmill description. 

The algorithm is very flexible. First, the restriction of a single-threaded mutator is not really important: as long as alloc(), advance(), readbarrier() and flip are mutually exclusive, no further constraints on concurrency are necessary. The mutator can be multi-threaded. The collector can be multi-threaded. advance() can be called "synchronously" (from alloc()), explicitly from the mutator code or "asynchronously" from the dedicated collector threads. A feedback-based method can regulate the frequency of calls to advance() depending on the amount of free and garbage objects. alloc() can penalise heavy-allocating threads forcing them to do most of the scanning, etc.

Next, when an object is grayed by darken(), all that matter is that the object is placed in the FRONT section. If darken() places the object next to top, then FRONT acts as a FIFO queue and the scan proceeds in the breadth-first order. If the object is placed next to scan then the scan proceeds in the depth-first order, which might result in a better locality of reference and better performance of a heap in virtual memory. A multi-threaded collector can use multiple FRONT lists, e.g., one per core and scan them concurrently.

New objects can be added to the heap at any time, by atomically linking them somewhere in the FREE list. Similarly, a bunch of objects can be at any moment atomically released from the FREE list with the usual considerations of fragmentation-avoidance in the lower layer allocator.

Support for variable-sized objects requires a separate cyclic list for each size (plus, perhaps an additional overflow list for very large objects). The top, bottom, scan and free pointers become arrays of pointers with an element for each size. If arbitrarily large objects (e.g., arrays) are supported then atomicity of advance() will require additional work: large objects need to be multi-coloured and will blacken gradually.

Forward and backward links to the cyclic list can be embedded in the object header or they can be stored separately, the latter might improve cache utilisation by the scanner.

References

[0] The Treadmill: Real-Time Garbage Collection Without Motion Sickness PDF (subscription), Postscript 

[1] List Processing in Real Time on a Serial Computer PDF 

[2] The Garbage Collection Handbook. The art of automatic memory management gchandbook.org 

[3] On-the-Fly Garbage Collection: An Exercise in Cooperation PDF

360 years later or „Скрещенья ног“

In 1896 Paul Gauguin completed Te Arii Vahine (The King’s Wife): From many similar paintings of his Tahitian period this, together with a couple of preparatory watercolours, is distinguished by artificial legs placement, which can be characterised in Russian by the equally forced line (quoted in this article's title) from a certain universally acclaimed poem. This strange posture is neither a deficiency nor an artistic whim. It is part of a silent, subtle game played over centuries, where moves are echoes and the reward—some flickering form of immortality: This is Diana Resting, by Cranach the Elder, 1537. Let me just note the birds and leave the pleasure of finding other clues to the reader. Lucas Cranach (and this is more widely known) himself played a very similar game with Dürer.

By sheer luck, the first painting is just few kilometers away from me in Pushkin's museum.