Treadmill is a "real-time" in-place garbage collection algorithm
designed by H. Baker [0]. It is simple, elegant, efficient and surprisingly
little known. Speaking of which, Mr. Baker's Wikipedia page
rivals one for an obscure Roman decadent poet in scarcity of information.
The general situation of garbage collection is that there is a program (called
a mutator in this case) that allocates objects (that will also be called nodes) in a
heap, which is a pool of memory managed by the garbage collector. The
mutator can update objects to point to other earlier allocated objects so that
objects form a graph, possibly with cycles. The mutator can store pointers to
objects in some locations outside of the heap, for example in the stack or in
the registers. These locations are called roots.
The mutator allocates objects, but does not frees them explicitly. It is the job
of the garbage collector to return unreachable objects, that is, the objects that
can not be reached by following pointers from the roots, back to the allocation
pool.
It is assumed that the collector, by looking at an object, can identify all
pointers to the heap stored in the object and that the collector knows all the
roots. If either of these assumptions does not hold, one needs a
conservative collector that can be implemented as a library for an
uncooperative compiler and run-time (e.g., Boehm garbage
collector for C and C++).
The earliest garbage collectors were part of Lisp
run-time. Lisp programs tend to allocate a large number of cons cells and organise them in
complex structures with cycles and sub-structure sharing. In fact, some of the
Lisp Machines had
garbage collection implemented in hardware and allocated everything including
stack frames and binding environments in the heap. Even processor instructions
were stored as cons cells in the heap.
To allocate a new object, the mutator calls alloc(). Treadmill is
"real-time" because the cost of alloc() in terms of processor cycles is
independent of the number of allocated objects and the total size of the heap,
in other words, alloc() is O(1) and this constant cost is not
high. This means garbage collection without "stop-the-world" pauses, at least as
long as the mutator does not genuinely exhaust the heap with reachable objects.
Treadmill is "in-place" because the address of an allocated object does not
change. This is in contrast with copying garbage collectors that can
move an object to a new place as part of the collection process (that implies some mechanism of updating the pointers to the moved object).
All existing garbage collection algorithms involve some form of scanning of
allocated objects and this scanning is usually described in terms of colours
assigned to objects. In the standard 3-colour scheme (introduced in [3] together
with the term "mutator"), black objects have been completely scanned together
with the objects they point to, gray objects have been scanned, but the
objects they point to are not guaranteed to be scanned and white objects
have not been scanned.
For historical reasons, Baker's papers colour free (un-allocated) objects white
and use black-gray-ecru instead
of black-gray-white. We stick with ecru, at least to get a chance to learn a fancy word.
Consider the simplest case first:
- the heap has a fixed size;
- the mutator is single-threaded;
- allocated objects all have the same size (like cons cells).
(All these restrictions will be lifted eventually.)
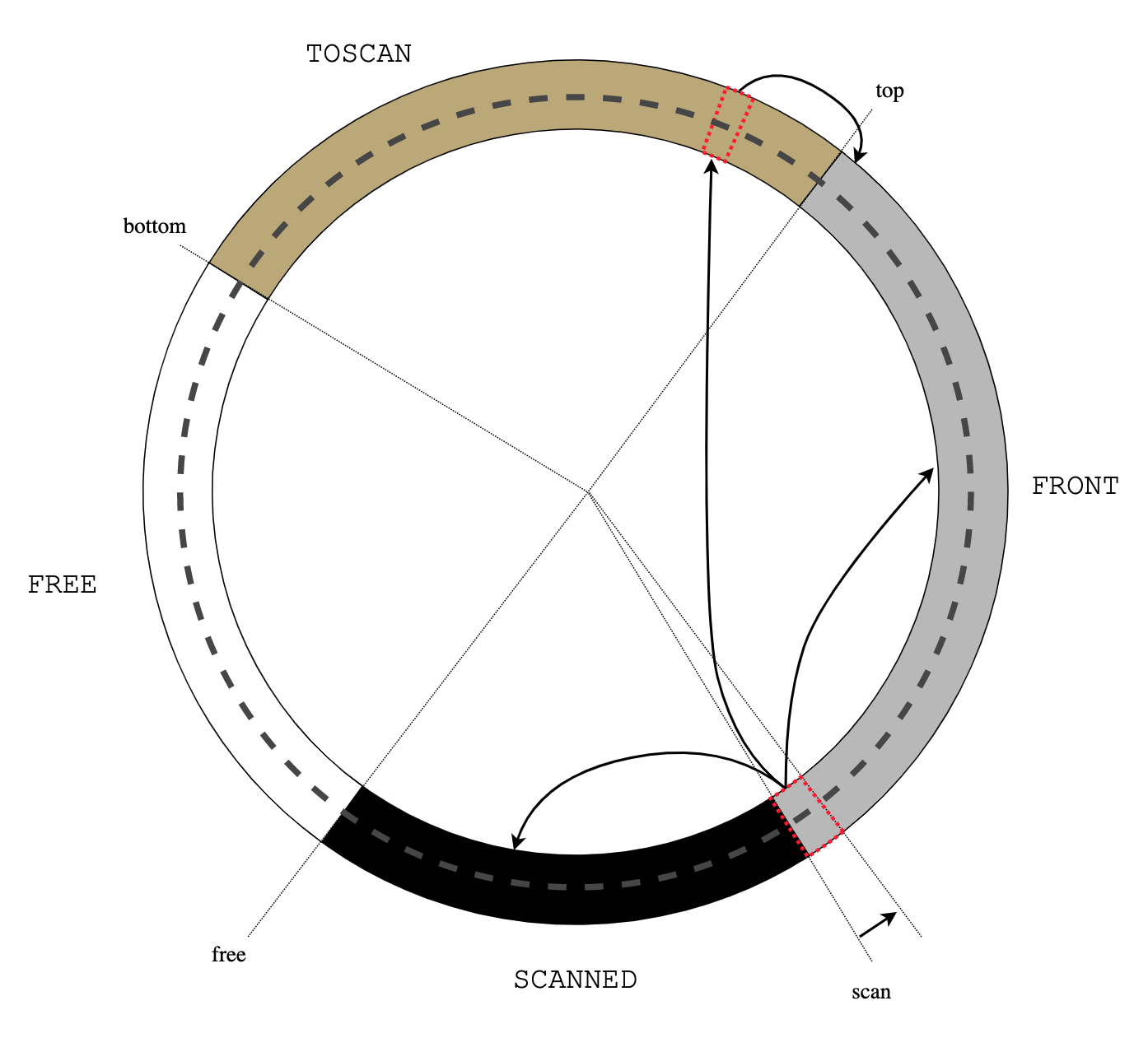
The main idea of treadmill is that all objects in the heap are organised in a
cyclic double-linked list, divided by 4 pointers into 4 segments:
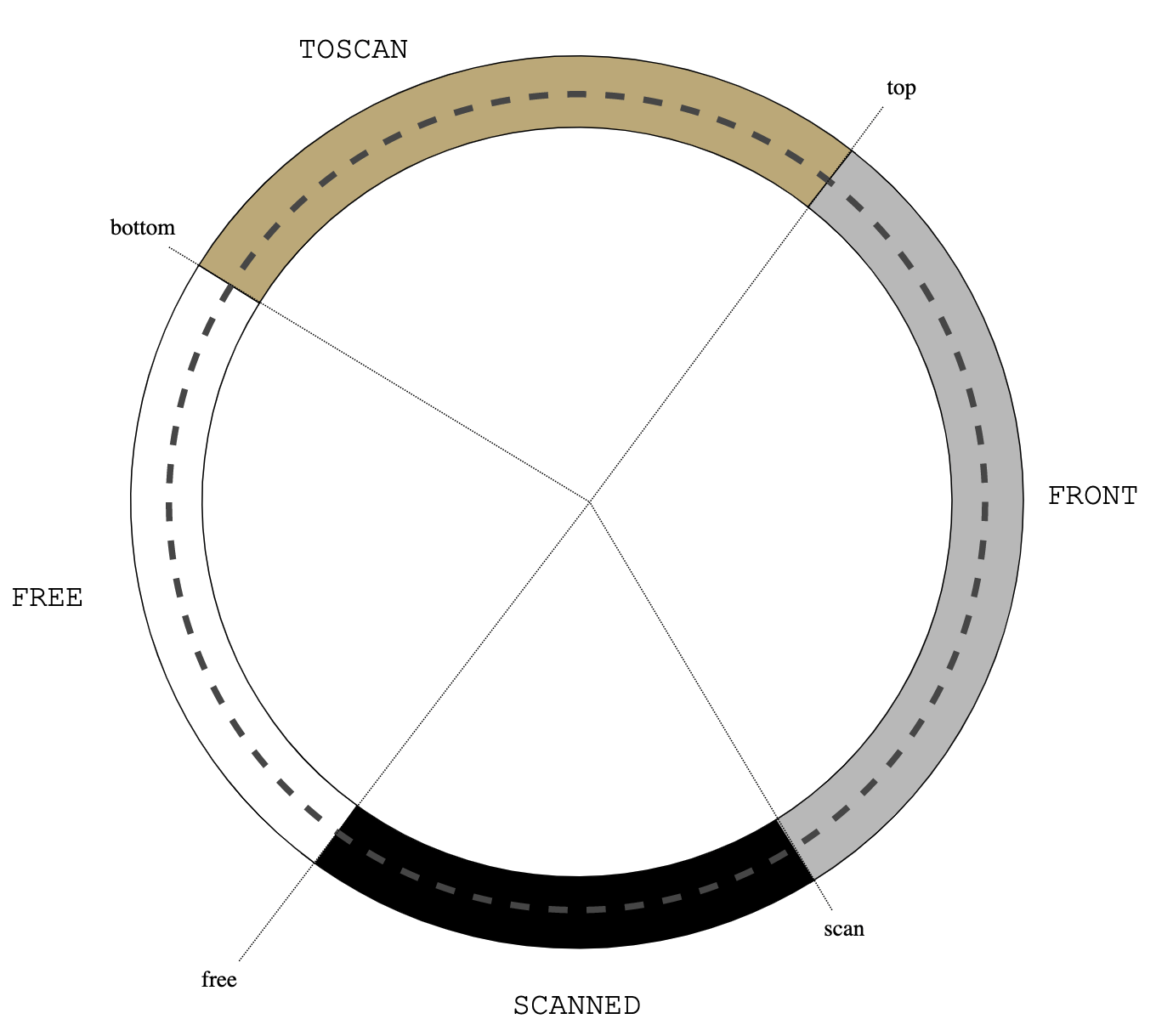 |
| Figure 0: treadmill |
Allocation of new objects happens at free (clockwise), scan advances at
scan (counterclockwise), still non-scanned objects are between
bottom and top (the latter 2 terms, somewhat confusing for a cyclic
list of objects, are re-used from an earlier paper [1], where a copying real-time
garbage collector was introduced).
Remarkably, the entire description and the proof of correctness of Treadmill
algorithm (and many other similar algorithms) depends on a single invariant:
Invariant: there are no pointers from black to ecru nodes.
That is, a black node can contain a pointer to another black node or to a gray
node. A non-black (that is, gray or ecru) node can point to any allocated node: black,
gray or ecru. An ecru node can be reached from a black node only through at least one intermediate gray node.
Let's for the time being postpone the explanation of why this invariant is important and instead discuss the usual 2 issues that any invariant introduces: how to establish it and how to maintain it.
Establishing is easy:
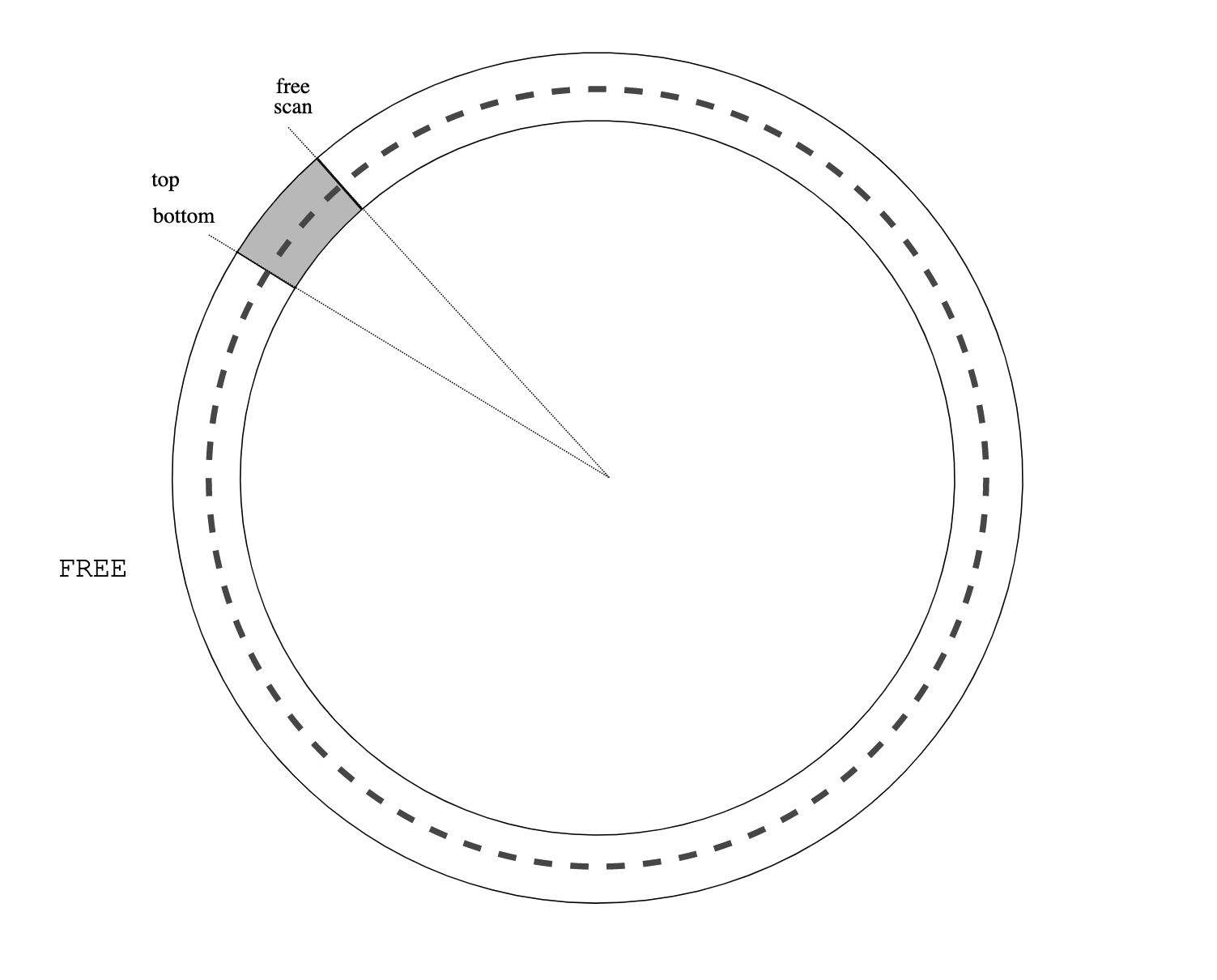 |
| Figure 1: initial heap state |
In the initial state, all objects are un-allocated (white), except for the roots that are gray. The invariant is satisfied trivially because there are no black objects.
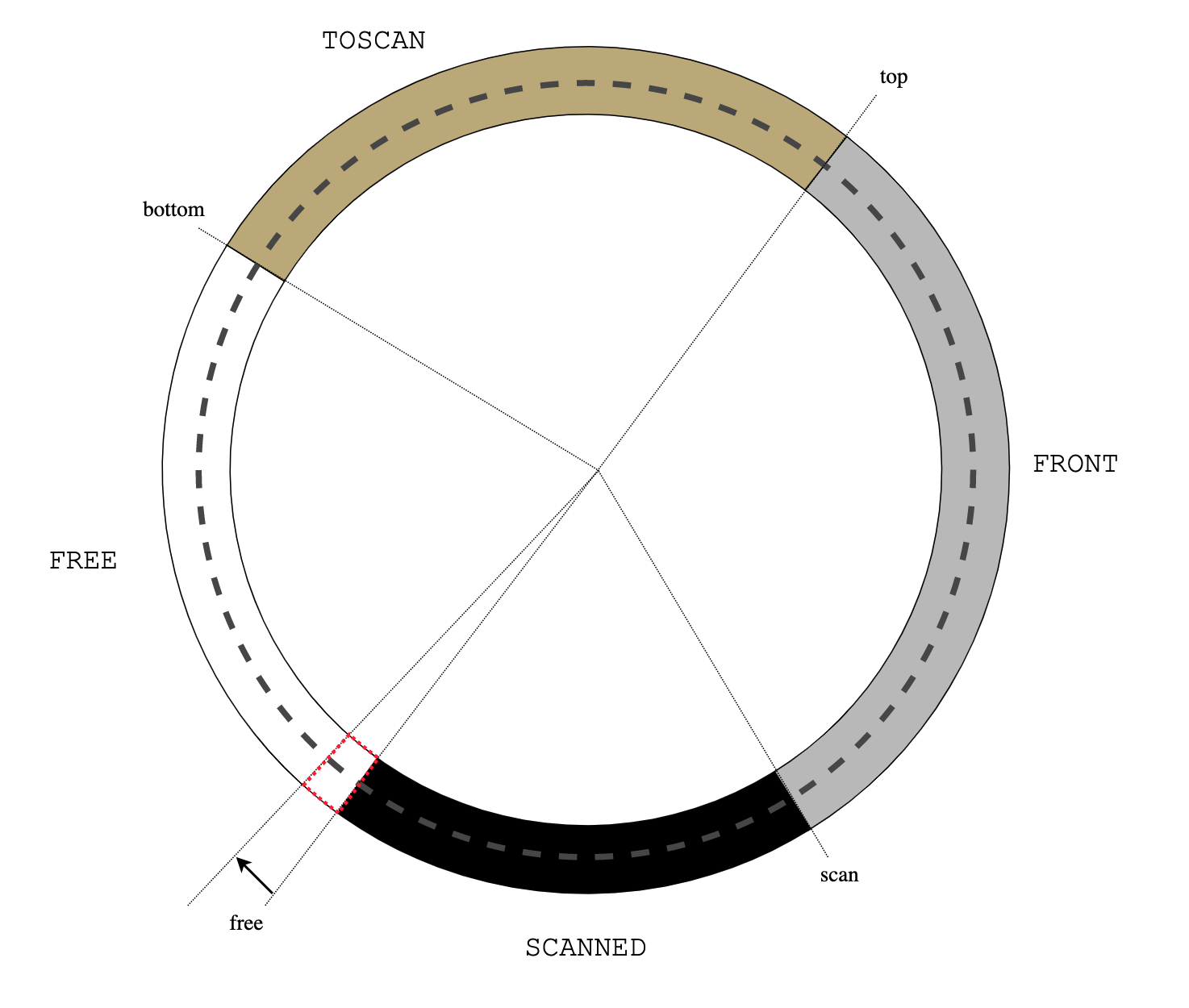 |
| Figure 2: alloc() |
Allocation cannot violate the invariant, because the newly allocated object does
not point to anything. In addition to calls to alloc() the mutator can
read pointer fields from nodes it already reached and update fields of reachable
nodes to point to other reachable nodes. There is no pointer arithmetic
(otherwise a conservative collector is needed). A reachable node is either
black, gray or ecru, so it seems, at the first sight, that the only way the
mutator can violate the invariant is by setting a field in a black object to
point to an ecru object. This is indeed the case with some collection algorithms
(called "gray mutator algorithms" in [2]). Such algorithms use
a write barrier, which is a special code inserted by the compiler
before (or instead of) updating a pointer field. The simplest write barrier
prevents a violation of the 3-colour invariant by graying the ecru target object if necessary:
writebarrier(obj, field, target) {
obj.field := target;
if black(obj) && ecru(target) {
darken(target);
}
}
darken(obj) { /* Make an ecru object gray. */
assert ecru(obj);
unlink(obj); /* Remove the object from the treadmill list. */
link(top, obj); /* Put it back at the tail of the gray list. */
}More sophisticated write barriers were studied that make use of the old value
of obj.field or are integrated with virtual memory sub-system, see [2] for details.
In our case, however, when the mutator reads a pointer field of an object, it
effectively stores the read value in a register (or in a stack frame slot) and
in Treadmill, registers can be black (Treadmill is a "black mutator
algorithm"). That is, the mutator can violate the invariant simply by reading
the pointer to an ecru object in a black register. To prevent this a read
barrier is needed, executed on every read of a pointer field:
readbarrier(obj, field) {
if ecru(obj) {
darken(obj);
}
return obj.field;
}
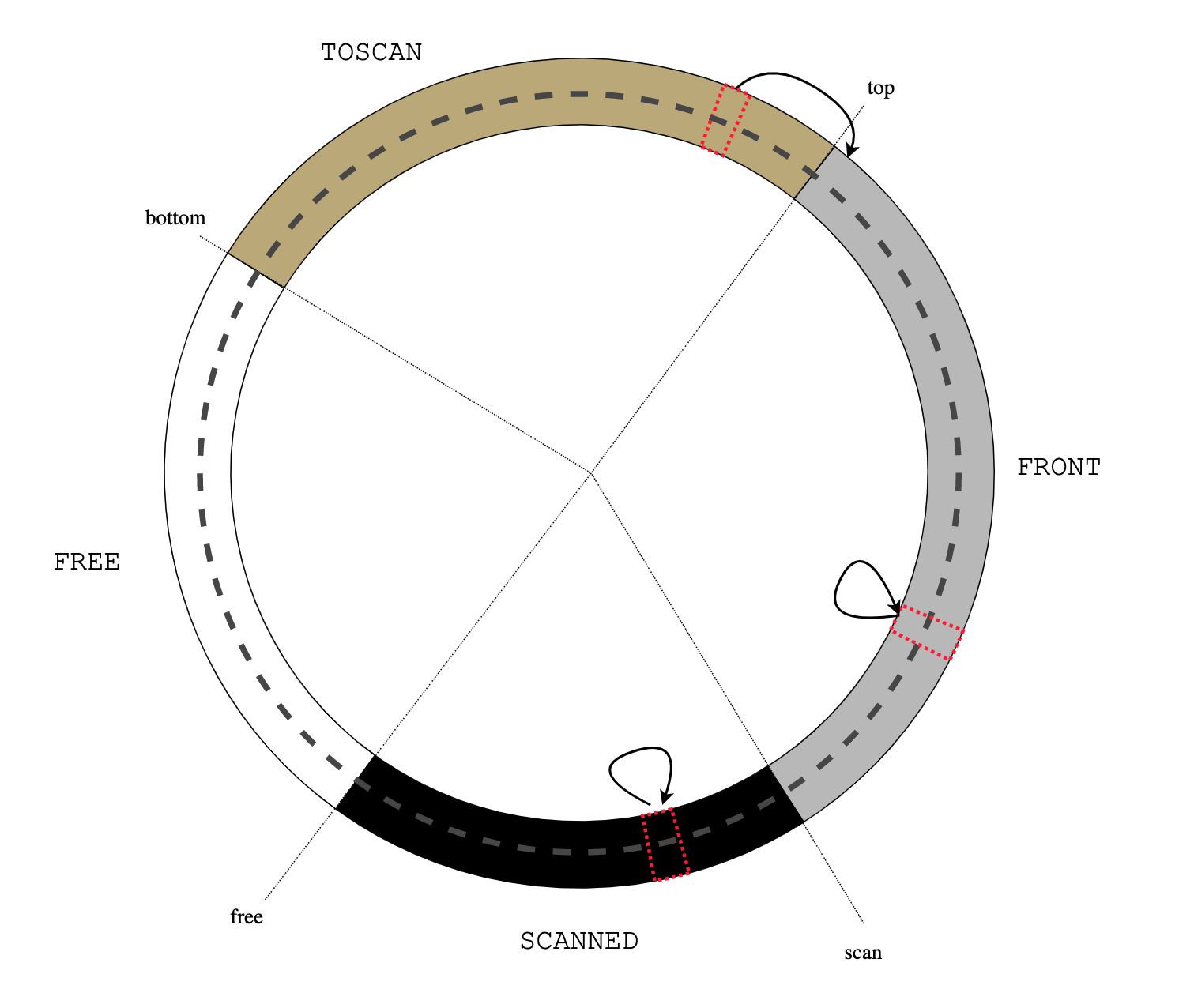
|
| Figure 3: read barrier |
That's how the invariant is established and maintained by the mutator. We still
haven't discussed how the collector works and where these mysterious ecru
objects appear from. The collector is very simple: it has a single entry point:
advance() { /* Scan the object pointed to by "scan". */
for field in pointers(scan) {
if ecru(scan.field) {
darken(scan.field);
}
}
scan := scan.prev; /* Make it black. */
}
advance() takes the gray object pointed to by scan, which is the head of the FRONT list, and grays all ecru objects that this object points to. After that, scan is advanced (counterclockwise), effectively moving the scanned object into the SCANNED section and making it black.
It's not important for now how
and when exactly advance() is called. What matters is that it blackens
an object while preserving the invariant.
Now comes the crucial part. An allocated object only darkens: the mutator
(readbarrier()) and the collector (advance()) can gray an ecru
object and advance() blackens a gray object. There is no way for a
black object to turn gray or for a gray object to turn ecru. Hence, the total
number of allocated non-black objects never increases. But advance()
always blackens one object, which means that after some number of calls
(interspersed with arbitrary mutator activity), advance() will run out
of objects to process: the FRONT section will be empty and there will be no gray
objects anymore:
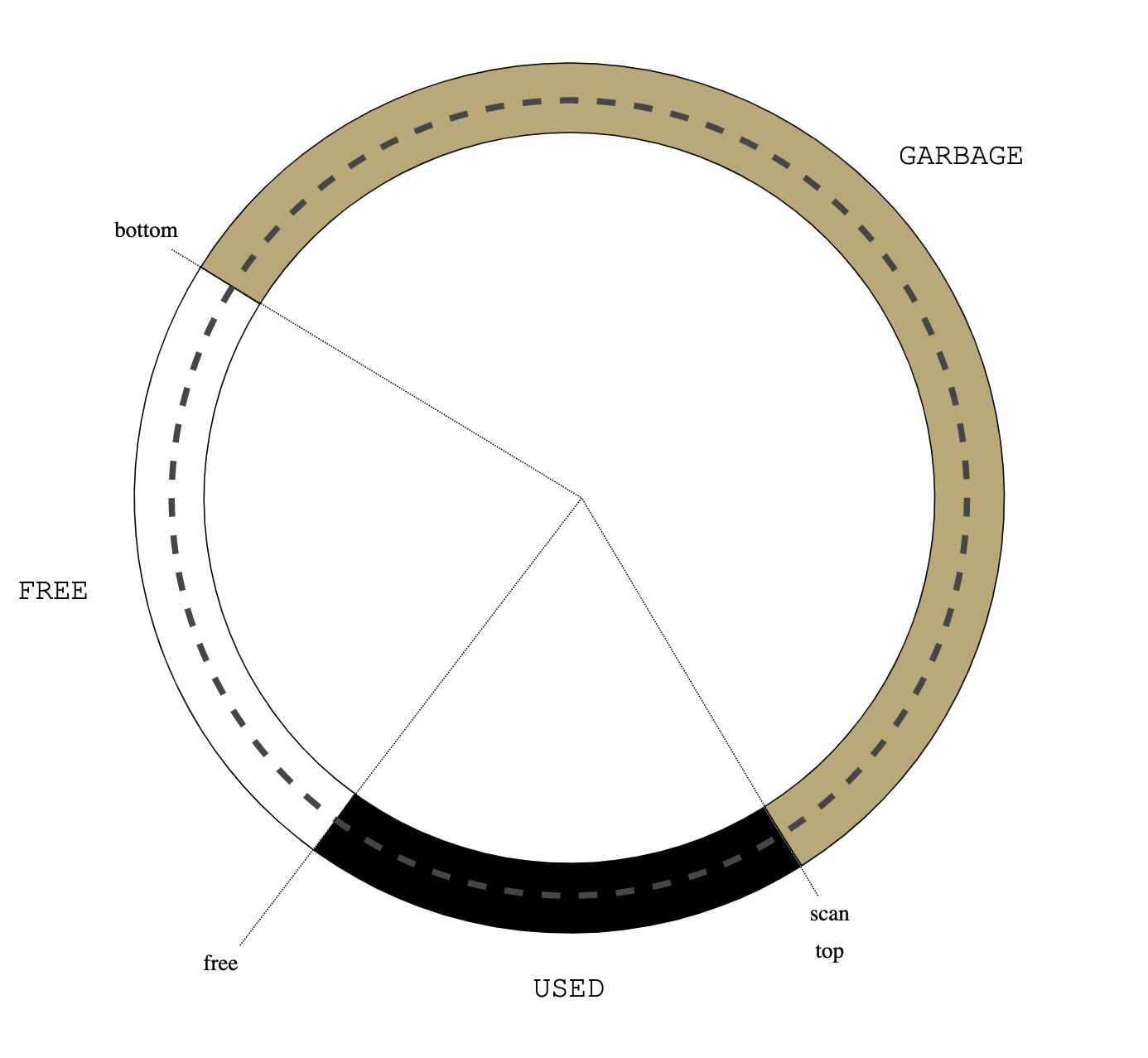 |
| Figure 5: no gray objects |
All roots were originally gray and could only darken, so they are now black. And
an ecru object is reachable from a black object only through a gray object, but
there are no gray objects, so ecru objects are not reachable from roots—they
are garbage. This completes the collection cycle and, in principle, it is
possible to move all ecru objects to the FREE list at that point and start the next
collection cycle. But we can do better. Instead of replenishing
the FREE list, wait until all objects are allocated and the FREE list is empty:
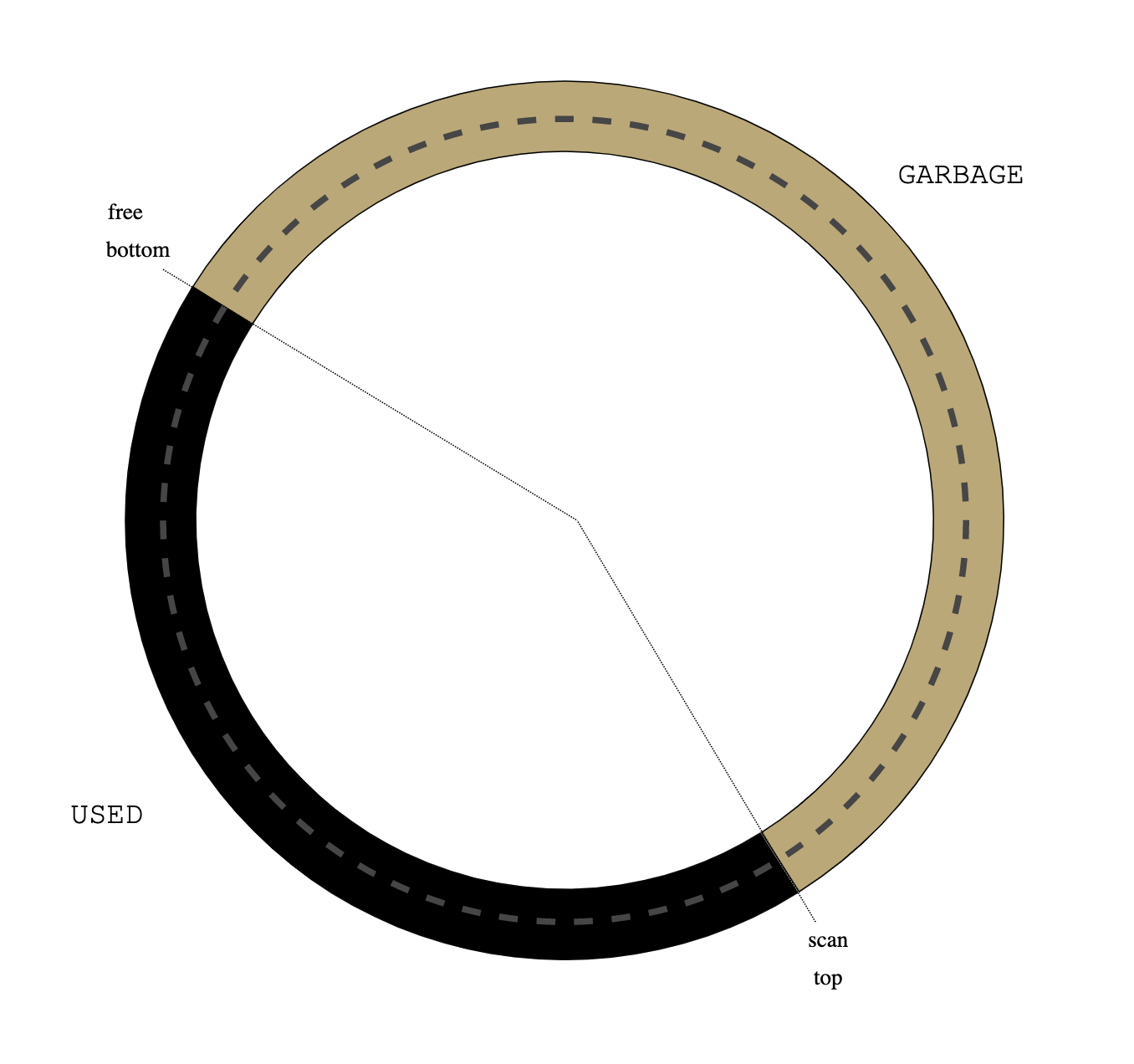 |
| Figure 6: neither gray nor white |
Only black and ecru objects remain. Flip them: swap top and bottom pointers and redefine colours: the old black objects are now ecru and the old ecru objects (remember they are garbage) are now white:
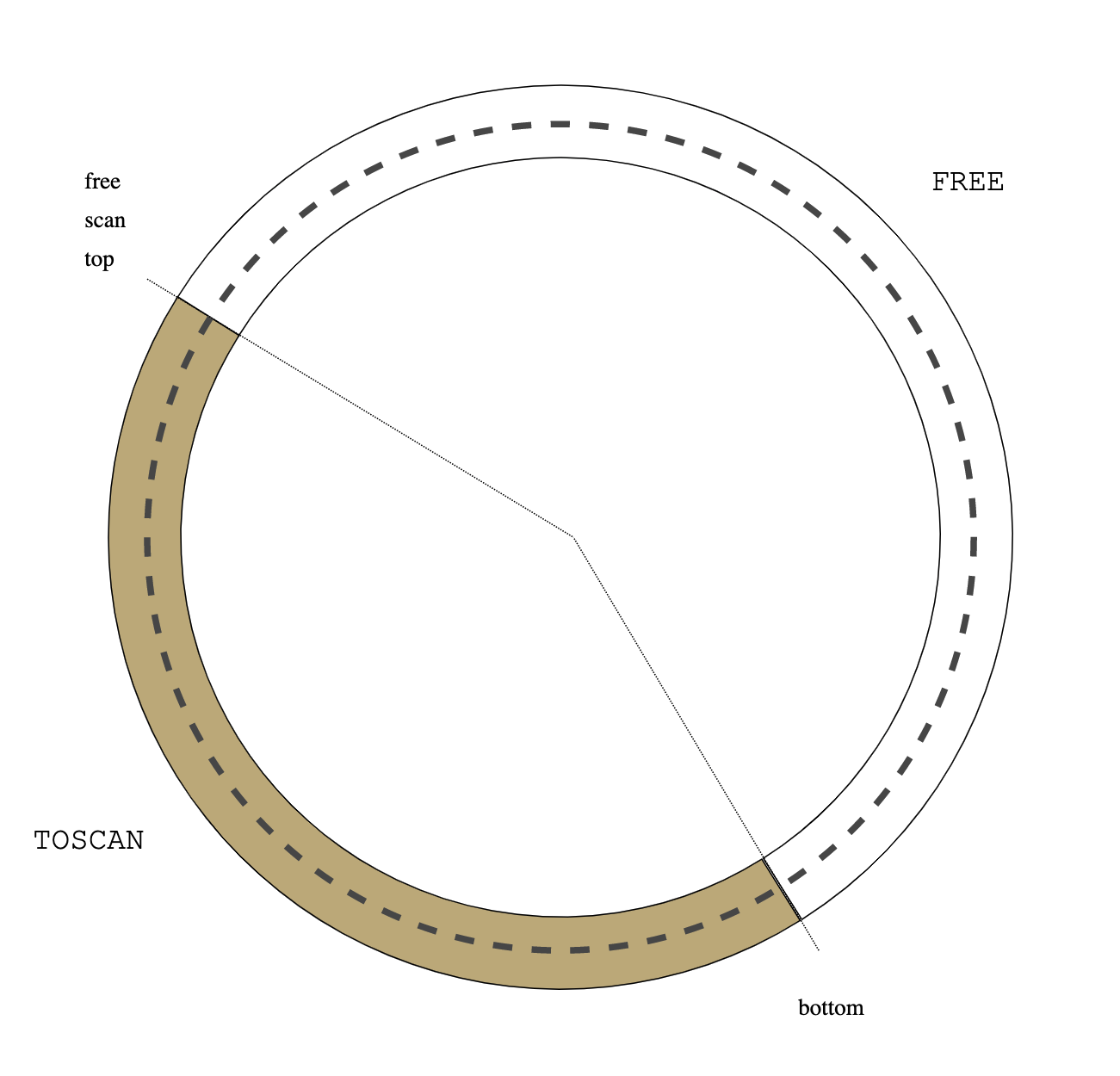 |
| Figure 7: flip |
The next collection cycle starts: put the roots between top and scan so that they are the new FRONT:
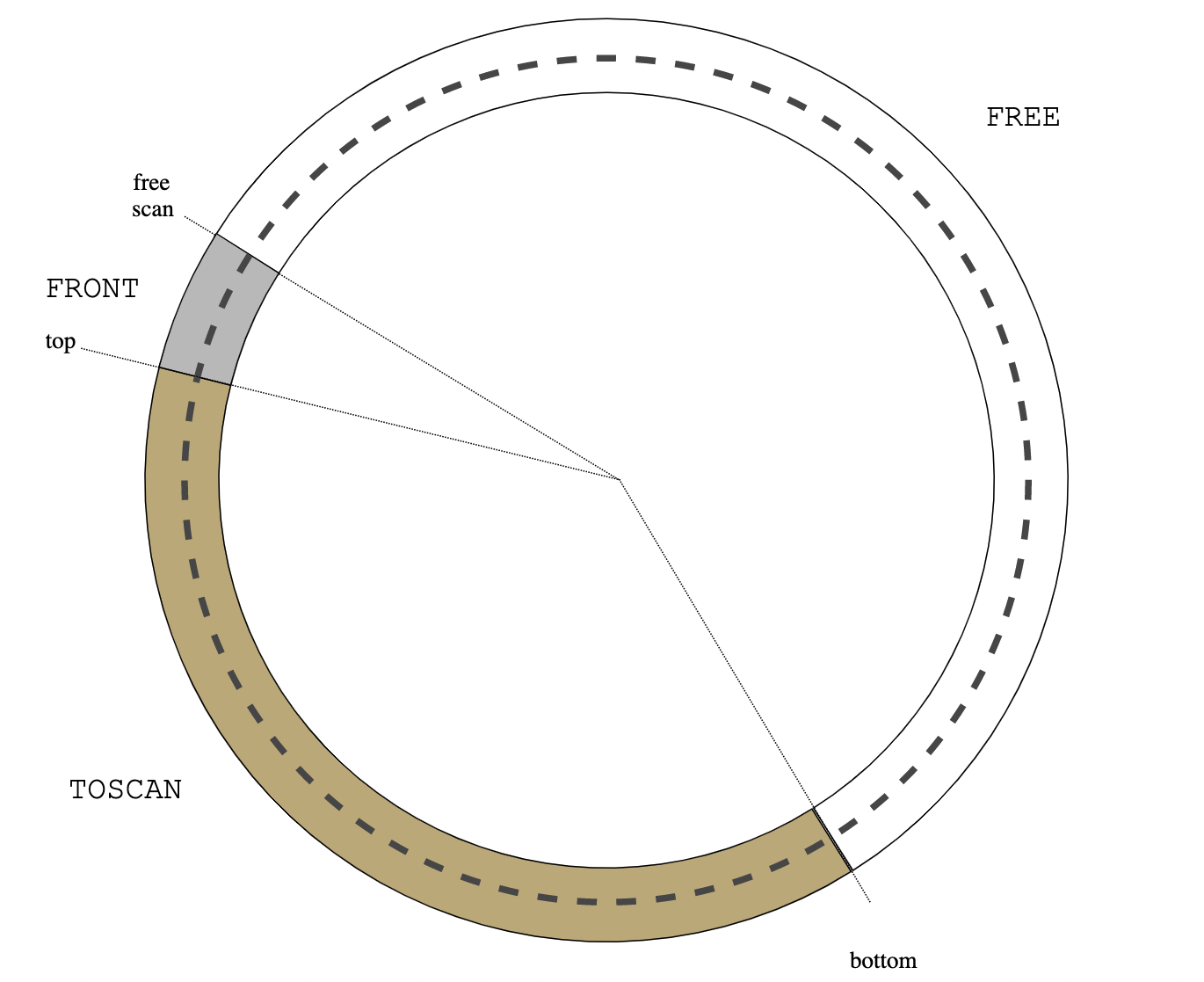 |
| Figure 8: new cycle |
From this point alloc() and advance() can continue as before.
Note that alloc(), advance() and readbarrier() do not
actually have to know object colour. They only should be able to tell an ecru
(allocated) object from non-ecru, so 1 bit of information per object is
required. By waiting until the FREE list is empty and re-defining colours Treadmill
avoids the need to scan the objects and change their colours at the end of a
collection cycle: it is completely O(1).
The last remaining bit of the puzzle is still lacking: how is it guaranteed that the
collection is completed before the FREE list is empty? If the mutator runs out of
free objects before the collection cycle is completed, then the only option is to
force the cycle to completion by calling advance() repeatedly until
there are no more gray objects and then flip, but that's a stop-the-world
situation.
The solution is to call advance() from within alloc()
guaranteeing scan progress. Baker proved that if advance() is called
k times for each alloc() call, then the algorithm never runs
out of free objects, provided that the total heap size is at least R*(1 +
1/k) objects, where R is the number of reachable objects.
This completes the Treadmill description.
The algorithm is very flexible. First, the restriction of a single-threaded
mutator is not really important: as long as alloc(), advance(), readbarrier()
and flip are mutually exclusive, no further constraints on concurrency are
necessary. The mutator can be multi-threaded. The collector can be
multi-threaded. advance() can be called "synchronously" (from
alloc()), explicitly from the mutator code or "asynchronously" from the
dedicated collector threads. A feedback-based method can regulate the frequency
of calls to advance() depending on the amount of free and garbage
objects. alloc() can penalise heavy-allocating threads forcing
them to do most of the scanning, etc.
Next, when an object is grayed by darken(), all that matter is that the
object is placed in the FRONT section. If darken() places the object
next to top, then FRONT acts as a FIFO queue and the scan proceeds in the
breadth-first order. If the object is placed next to scan then the scan
proceeds in the depth-first order, which might result in a better locality of
reference and better performance of a heap in virtual memory. A multi-threaded collector can use multiple FRONT lists, e.g., one per core and scan them
concurrently.
New objects can be added to the heap at any time, by atomically linking them
somewhere in the FREE list. Similarly, a bunch of objects can be at any moment
atomically released from the FREE list with the usual considerations of
fragmentation-avoidance in the lower layer allocator.
Support for variable-sized objects requires a separate cyclic list for each size
(plus, perhaps an additional overflow list for very large objects). The
top, bottom, scan and free pointers become
arrays of pointers with an element for each size. If arbitrarily large objects
(e.g., arrays) are supported then atomicity of advance() will
require additional work: large objects need to be multi-coloured and will blacken gradually.
Forward and backward links to the cyclic list can be embedded in the object
header or they can be stored separately, the latter might improve cache
utilisation by the scanner.
References
[0] The Treadmill: Real-Time Garbage Collection Without Motion Sickness PDF (subscription), Postscript[1] List Processing in Real Time on a Serial Computer
PDF
[2] The Garbage Collection Handbook. The art of automatic memory management
gchandbook.org
[3] On-the-Fly Garbage Collection: An Exercise in Cooperation
PDF
Sorry for the offtop but that's a pretty website.
ReplyDeleteNice. I look forward to investigating this more. I'm writing a small runtime, and this could be very useful.
ReplyDelete